1927. Area in Triangle
Given a triangle field and a rope of a certain length,
you are required to use the rope to enclose a region within the field and make
the region as large as possible.
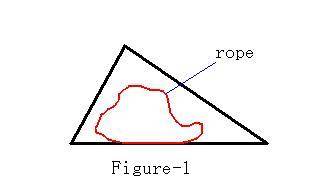
Input. The input has several sets of test data. Each set is
one line containing four numbers separated by a space. The first three indicate
the lengths of the edges of the triangle field, and the fourth is the length of
the rope. Each of the four numbers have exactly four digits after the decimal
point. The line containing four zeros ends the input and should not be
processed. You can assume each of the edges are not longer than 100.0000 and
the length of the rope is not longer than the perimeter of the field.
Output. Output one line for each case in the following format:
Case i: X
Where i is the case number, and X is the largest area which is rounded to
two digits after the decimal point.
Sample Input
12.0000
23.0000 17.0000 40.0000
84.0000
35.0000 91.0000 210.0000
100.0000
100.0000 100.0000 181.3800
0 0 0 0
Sample
Output
Case 1:
89.35
Case 2:
1470.00
Case 3:
2618.00
РЕШЕНИЕ
геометрия
Анализ алгоритма
Если длина веревки d больше периметра треугольника (L = a
+ b + c), то ответом будет площадь треугольника.
Пусть окружность, вписанная
в треугольник, имеет радиус r. Если
длина веревки d не больше длины этой
окружности 2 π r, то веревку
следует выложить в виде окружности с длиной d.
Радиус r' такой окружности найдем из
соотношения 2 π r‘ = d. Откуда r’ = d / 2 π. Площадь окружности составит π r’2 = ![]() =
= ![]() .
.
Если длина веревки d больше длины вписанной в треугольник
окружности, то ее следует расположить следующим образом:
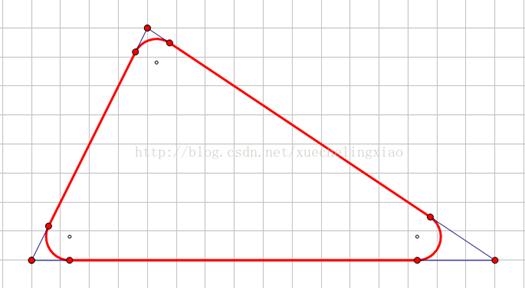
Если три дуги возле углов
треугольника сложить вместе, то получится окружность (все три дуги имеют один
радиус). Проведем XY || AB. Впишем окружность в треугольник YXC. Ее длина равна
сумме длин трех дуг, радиус равен r'.
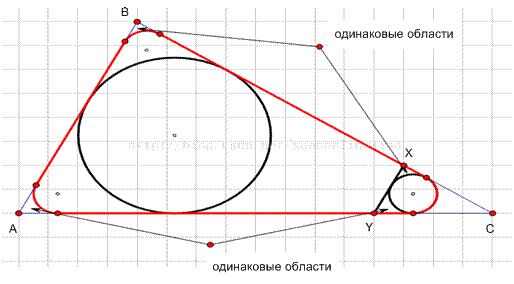
L – d = PYXC
– 2 π r’ = Lt – 2 π r t, где t – коэффициент подобия треугольников ABC и YXC. Отсюда t = (L
– d) / (L – 2 π r). Радиус окружности, вписанной в
треугольник YXC, равен r' = rt.
Площадь области, окруженной
веревкой, равна площади треугольника ABC минус площадь треугольника YXC плюс
площадь круга, вписанного в треугольник YXC.
Реализация алгоритма
#include <stdio.h>
#include <math.h>
#define Pi
acos (-1.0)
int main(void)
{
double a, b,
c, d;
int test = 1;
while (scanf
("%lf %lf %lf %lf", &a, &b,
&c, &d), a + b + c + d != 0)
{
double L =
a + b + c;
double cosA
= (b * b + c * c - a * a) / (2 * b * c);
double S =
0.5 * b * c * (sqrt (1-cosA * cosA));
double r =
S * 2 / L;
double ans;
if (d >
L)
{
ans = S;
}
else if (2 * Pi * r >= d)
{
ans = d * d / (4 * Pi);
}
else
{
double t
= (L - d) / (L - 2 * Pi * r);
double rr
= r * t;
ans = S - S * t * t + Pi * rr * rr;
}
printf ("Case%
d:% .2lf\n", test++, ans);
}
return 0;
}