2323. PERMS
Count the number of permutations that
have a specific number of inversions.
Given a permutation a1, a2, a3,...,
an of the n integers 1, 2, 3, ..., n, an inversion is a pair (ai, aj) where i
< j and ai > aj.
The number of inversions in a permutation gives an indication on how
"unsorted" a permutation is. If we wish to analyze the average
running time of a sorting algorithm, it is often useful to know how many
permutations of n objects will have a
certain number of inversions.
In this problem you are asked to
compute the number of permutations of n
values that have exactly k
inversions.
For example, if n = 3, there are 6 permutations with the indicated inversions as
follows:
123 0 inversions
132 1 inversion (3 > 2)
213 1 inversion (2 > 1)
231 2 inversions (2 > 1, 3 > 1)
312 2 inversions (3 > 1, 3 > 2)
321 3 inversions (3 > 2, 3 > 1, 2
> 1)
Therefore, for the permutations of 3
things
1 of them
has 0 inversions
2 of them
have 1 inversion
2 of them
have 2 inversions
1 of them
has 3 inversions
0 of them
have 4 inversions
0 of them
have 5 inversions
etc.
Input. The input
consists one or more problems. The input for each problem is specified on a
single line, giving the integer n (1
≤ n ≤ 18) and a
non-negative integer k (0 ≤ k ≤ 200). The end of input is
specified by a line with n = k = 0.
Output. For each
problem, output the number of permutations of {1, ..., n} with exactly k
inversions.
|
Sample input |
Sample output |
|
3 0 3 1 3 2 3 3 4 2 4 10 13 23 18 80 0 0 |
1 2 2 1 5 0 46936280 184348859235088 |
РЕШЕНИЕ
последовательности
- инверсии
Анализ алгоритма
Пусть f(n, k) – количество
перестановок из n элементов с k инверсиями. Тогда очевидно, что:
·
f(0,
k) = 0, так как перестановки длины 0
не существует;
·
f(n, 0) = 1, это единственная перестановка
(1, 2, 3, …, n)
·
f(n, n
* (n – 1) / 2) = 1, это единственная
перестановка (n, n – 1, n – 2, …, 1)
·
f(n, k) =
0 при k > n * (n – 1) / 2
Рассмотрим все перестановки из n элементов с k инверсиями, число которых равно f(n, k). У нас имеется n + 1 позиция для вставки числа n + 1 для получения перестановки из n + 1 элемента. Пусть происходит вставка
числа n + 1 в i-ую позицию справа (1 ≤ i
≤ n + 1). Например, при i = 1 вставка происходит справа, при i = n
+ 1 слева. Тогда полученная перестановка будет иметь k + i – 1 инверсий. Это значит, что значение f(n, k)
следует прибавить к f(n + 1, k + i
– 1), 1 ≤ i ≤ n + 1.
Например:
·
f(2,
0) следует прибавить к f(3, 0), f(3, 1) и f(3, 2),
·
f(2,
1) следует прибавить к f(3, 1), f(3, 2) и f(3, 3).
С другой стороны можно заметить, что
f(n,
k) =![]()
Например (учитывая, что f(2,
k) = 0 при k
> 1):
·
f(3, 0) = ![]() = f(2, 0) = 1,
= f(2, 0) = 1,
·
f(3, 1) = ![]() = f(2, 1) + f(2,
0) = 1 + 1 = 2,
= f(2, 1) + f(2,
0) = 1 + 1 = 2,
·
f(3, 2) = ![]() = f(2, 2) + f(2,
1) + f(2, 0) = 0 + 1 + 1 = 2,
= f(2, 2) + f(2,
1) + f(2, 0) = 0 + 1 + 1 = 2,
·
f(3, 3) = ![]() = f(2, 3) + f(2,
2) + f(2, 1) = 0 + 0 + 1 = 1.
= f(2, 3) + f(2,
2) + f(2, 1) = 0 + 0 + 1 = 1.
Пример
Рассмотрим все перестановки при n = 2. Существует одна перестановка (1,
2) с нуль инверсиями и одна перестановка (2, 1) с одной инверсией:

Для вычисления f(3, k)
будем вставлять число 3 во все позиции перестановок с n = 2. Например, возьмем перестановку
(1, 2) и будем вставлять 3 во все возможные позиции. Это значит, что f(2, 0) =
1 следует прибавить к:
·
f(3,
0), получим перестановку (1, 2, 3)
·
f(3,
1), получим перестановку (1, 3, 2)
·
f(3,
2), получим перестановку (3, 1, 2)
Теперь возьмем перестановку (2, 1) и
будем вставлять 3 во все возможные позиции. Это значит, что f(2, 1) = 1 следует
прибавить к:
·
f(3,
1), получим перестановку (2, 1, 3)
·
f(3,
2), получим перестановку (2, 3, 1)
·
f(3,
3), получим перестановку (3, 2, 1)

Реализация алгоритма
#include <stdio.h>
#define MaxN 19
#define MaxK 201
long long
dp[MaxN][MaxK]= {0};
int i, n, k;
int main(void)
{
dp[1][0] = 1;
for(n = 1; n < MaxN - 1; n++)
for(k = 0; dp[n][k] > 0; k++)
for(i = 1; i <= n + 1; i++)
dp[n+1][k+i-1] += dp[n][k];
while(scanf("%d
%d",&n,&k), n + k)
printf("%lld\n",dp[n][k]);
}
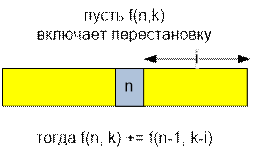
Реализация алгоритма при помощи рекуррентности
#include <stdio.h>
#include <string.h>
#define MaxN 19
#define MaxK 201
long long
dp[MaxN][MaxK]= {0};
int i, n, k;
int min(int
i, int j)
{
return (i < j) ? i : j;
}
long long
f(int n, int k)
{
if (dp[n][k] != -1) return
dp[n][k];
if (n == 0) return
dp[n][k] = 0;
if (k == 0) return
dp[n][k] = 1;
if (k > n * ( n - 1) / 2) return
dp[n][k] = 0;
dp[n][k] = 0;
for(int i = 0; i
<= min(n - 1, k); i++)
dp[n][k] += f(n-1,k
- i);
return dp[n][k];
}
int main(void)
{
memset(dp,-1,sizeof(dp));
while(scanf("%d
%d",&n,&k), n + k)
printf("%lld\n",f(n,k));
}