3321. Apple Tree

There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

The tree has n forks which are connected by branches. Kaka numbers the forks by 1 to n and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input. The first line contains an integer n (n ≤ 100,000) , which is the number of the forks in the tree. The following n – 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.

The next line contains an integer m (m ≤ 100,000). The following m lines each contain a message which is either

· "C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork

· "Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x

Note the tree is full of apples at the beginning.

Output. For every inquiry, output the correspond answer per line.

Sample input	Sample output
3 1 2 1 3 3 Q 1 C 2 Q 1	3 2

РЕШЕНИЕ

дерево Фенвика

Анализ алгоритма

Запустим поиск в глубину и в порядке посещения вершин перенумеруем их, например начиная с 1. Номер i-ой вершины сохраним в start[i]. Рассмотрим поддерево с корнем v. Пусть в результате обхода в глубину все его вершины получили номера от start[v] до cnt. Заведем еще один массив end и положим end[v] = cnt. Тогда все вершины поддерева с корнем v (включая и саму вершину v) имеют номера от start[v] до end[v].

Пусть apples – масив состояния яблок на дереве, изначально он содержит все единицы (apples[i] содержит количество яблок в i-ой вершине). Сумма яблок в поддереве с корнем v равно apples[start[v]] + … + apples[end[v]]. Построим по массиву apples дерево Фенвика чтобы вычислять указанную сумму за O(logn).

Пример

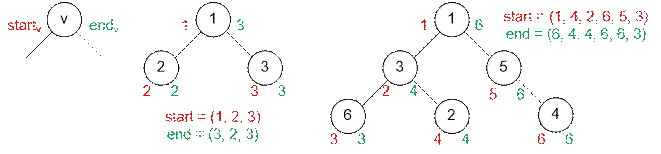
Реализация алгоритма

#include <cstdio>

#include <vector>

#define MAX 100010

using namespace std;

int Fenwick[MAX];

int i, n, m, x, u, v, cnt;

char ch;

vector<vector<int> > g;

vector<int> start, end, apple;

// fill Fenwick array for a = [1, 1, ..., 1] - apples everywhere

void Init(void)

{

for(i = 0; i <= n; i++)

Fenwick[i] = (i + 1) & (-i - 1);

}

// Fenwick[0] + Fenwick[1] + ... + Fenwick[i]

int Summma0_i(int i)

{

int result = 0;

for (; i >= 0; i = (i & (i + 1)) - 1)

result += Fenwick[i];

return result;

}

// Fenwick[i] = Fenwick[i] + delta

void IncElement(int i, int delta)

{

for (; i <= n; i = (i | (i+1)))

Fenwick[i] += delta;

}

void dfs(int v, int p = -1)

{

start[v] = cnt++;

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (to != p) dfs(to,v);

}

end[v] = cnt - 1;

}

int main (void)

{

scanf("%d",&n);

Init();

g.resize(n+1);

for(i = 0; i < n - 1; i++)

{

scanf("%d %d",&u,&v);

g[u].push_back(v);

g[v].push_back(u);

}

start.resize(n+1); end.resize(n+1);

apple.assign(n+1,1);

cnt = 1;

dfs(1);

scanf("%d\n",&m);

for(i = 0; i < m; i++)

{

scanf("%c %d\n",&ch,&x);

if (ch == 'Q')

printf("%d\n",Summma0_i(end[x]) - Summma0_i(start[x]-1));

else

{

IncElement(start[x],apple[x] ? -1 : 1);

apple[x] ^= 1;

}

}

return 0;

}