3692. Kindergarten

In a kindergarten, there are a lot of kids. All girls of the kids know each other and all boys also know each other. In addition to that, some girls and boys know each other. Now the teachers want to pick some kids to play a game, which need that all players know each other. You are to help to find maximum number of kids the teacher can pick.

Input. The input consists of multiple test cases. Each test case starts with a line containing three integers G, B (1 ≤ G, B ≤ 200) and M (0 ≤ M ≤ G × B), which is the number of girls, the number of boys and the number of pairs of girl and boy who know each other, respectively.

Each of the following M lines contains two integers X and Y (1 ≤ X ≤ G, 1 ≤ Y ≤ B), which indicates that girl X and boy Y know each other.

The girls are numbered from 1 to G and the boys are numbered from 1 to B.

The last test case is followed by a line containing three zeros.

Output. For each test case, print a line containing the test case number( beginning with 1) followed by a integer which is the maximum number of kids the teacher can pick.

Sample input	Sample output
2 3 3 1 1 1 2 2 3 2 3 5 1 1 1 2 2 1 2 2 2 3 0 0 0	Case 1: 3 Case 2: 4

РЕШЕНИЕ

графы - паросочетания

Анализ алгоритма

Кликой в неориентированном графе называется подмножество вершин, каждые две из которых соединены ребром графа. Кликой является полный подграф первоначального графа. Размер клики определяется как число вершин в ней.

Задача о клике существует в двух вариантах:

· в задаче распознавания требуется определить, существует ли в заданном графе G клика размера k

· в вычислительном варианте требуется найти в заданном графе G клику максимального размера.

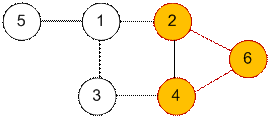
Максимальная клика графа G имеет размер 3

Множество вершин графа называется независимым (Independent Set), если никакие две вершины этого множества не соединены ребром. То есть ндуцированный этим множеством подграф состоит из изолированных вершин. Каждое ребро графа инцидентно не более чем одной вершине из независимого множества.

Задача о независимом множестве существует в двух вариантах:

· в задаче распознавания требуется определить, существует ли в заданном графе G независимое множество размера k.

· в задаче о независимом множестве требуется найти в заданном графе G независимое множество максимального размера. Этот размер называют числом независимости.

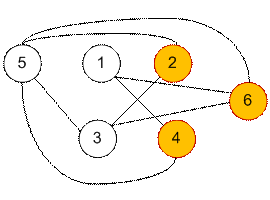
Максимальное независимое множество дополнения графа G имеет размер 3

Задача о независимом множестве и задача о клике являются двойственными: клика в G – это независимое множество в дополнении графа G и наоборот.

Необходимым и достаточным условием для существования клики размера k является наличие независимого множества размера не менее k в дополнении графа. Полнота подграфа означает, что его дополнение не содержит ни одного ребра.

В нашей задаче в заданном графе следует найти максимальную клику. При этом известно, что левая и правая части графа являются полными подграфами (все мальчики знают друг друга и все девочки знают друг друга). Размер максимальной клики равен размеру максимального независимого множества дополнения графа.

Дополнением к имеющемуся графу будет двудольный граф. В двудольных графах все вершины, не входящие в минимальное вершинное покрытие, могут быть включены в максимальное независимое множество. То есть

размер максимального независимого множества =

количество вершин графа – размер минимального вершинного покрытия

Теорема Кенига. В двудольном графе размер максимального паросочетания равен размеру минимального вершинного покрытия.

Из теоремы Кенига следует, что

размер максимальной клики =

размер максимального независимого множества в дополняющем графе =

количество вершин графа – размер минимального вершинного покрытия =

количество вершин графа – размер максимального паросочетания в дополняющем графе

Пример

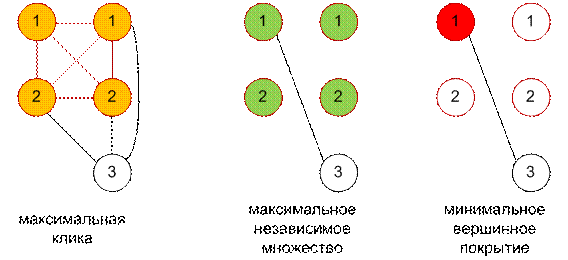
Рассмотрим второй пример. Размер максимальной клики графа равен 4. Размер максимального независимого множества в дополняющем графе равен 4.

Реализация алгоритма

#include <stdio.h>

#include <string.h>

#define MAX 210

int gr[MAX][MAX];

int used[MAX], mt[MAX], par[MAX];

int i, j, ptr;

int g, b, m, x, y, cs, flow;

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 1; i <= b; i++)

{

if (gr[v][i] == 1) continue;

if (mt[i] == -1 || dfs(mt[i]))

{

mt[i] = v;

par[v] = 1;

return 1;

}

}

return 0;

}

void AugmentingPath(void)

{

int i, run;

memset(mt,-1,sizeof(mt));

memset(par,-1,sizeof(par));

for (run = 1; run; )

{

run = 0;

memset(used,0,sizeof(used));

for (i = 1; i <= g; i++)

if ((par[i] == -1) && dfs(i)) run = 1;

}

}

int main(void)

{

cs = 1;

while(scanf("%d %d %d",&g,&b,&m), g + b + m > 0)

{

memset(gr,0,sizeof(gr));

for(i = 0; i < m; i++)

{

scanf("%d %d",&x,&y);

gr[x][y] = 1;

}

AugmentingPath();

for (flow = 0, i = 1; i <= b; i++)

if (mt[i] != -1) flow++;

printf("Case %d: %d\n",cs++,g + b - flow);

}

return 0;

}