1674. Sorting by Swapping

Given a permutation of numbers from 1 to n, we can always get the sequence 1, 2, 3, ..., n by swapping pairs of numbers. For example, if the initial sequence is 2, 3, 5, 4, 1, we can sort them in the following way:

2 3 5 4 1

1 3 5 4 2

1 3 2 4 5

1 2 3 4 5

Here three swaps have been used. The problem is, given a specific permutation, how many swaps we needs to take at least.

Input. The first line contains a single integer t (1 ≤ t ≤ 20) that indicates the number of test cases. Then follow the t cases. Each case contains two lines. The first line contains the integer n (1 ≤ n ≤ 10000), and the second line gives the initial permutation.

Output. For each test case, the output will be only one integer, which is the least number of swaps needed to get the sequence 1, 2, 3, ..., n from the initial permutation.

Sample Input	Sample Output
2 3 1 2 3 5 2 3 5 4 1	0 3

РЕШЕНИЕ

сортировка

Анализ алгоритма

Представим перестановку в виде объединения множества циклов. Числа в каждом цикле можно упорядочить за k – 1 обменов, где k – длина цикла.

Пример

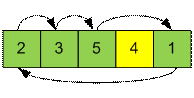
Перестановка (2, 3, 5, 4, 1) раскладывается на два цикла: (2, 3, 5, 1) и (4). Числа в первом цикле можно отсортировать за 3 перестановки. Второй цикл уже отсортирован.

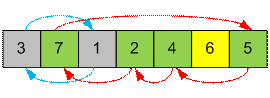
Перестановка (3, 7, 1, 2, 4, 6, 5) раскладывается на три цикла: (3, 1), (7, 5, 4, 2) и (6). Числа в первом цикле можно отсортировать за 1 перестановку, во втором за 3. Третий цикл уже отсортирован.

Реализация алгоритма

#include <stdio.h>

#define MAX 10010

int i, n, tests, cnt, u, temp;

int m[MAX];

int main(void)

{

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&m[i]);

cnt = 0;

for(i = 1; i <= n; i++)

if (m[i] != i)

{

u = i;

while(m[u] != u)

{

temp = m[u];

m[u] = u;

u = temp;

cnt++;

}

cnt--;

}

printf("%d\n",cnt);

}

return 0;

}