3266. K-query

Given a sequence of n numbers a₁, a₂, ..., a_n and a number of k- queries. A k-query is a triple (i, j, k) (1 ≤ i ≤ j ≤ n). For each k-query (i, j, k), you have to return the number of elements greater than k in the subsequence a_i, a_i+1, ..., a_j.

Input.

Line 1: n (1 ≤ n ≤ 30000).

Line 2: n numbers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹).

Line 3: q (1 ≤ q ≤ 200000), the number of k-queries.

In the next q lines, each line contains 3 numbers i, j, k representing a k-query (1 ≤ i ≤ j ≤ n, 1 ≤ k ≤ 10⁹).

Output. For each k-query (i, j, k), print the number of elements greater than k in the subsequence a_i, a_i+1, ..., a_j in a single line.

Sample Input

5

5 1 2 3 4

3

2 4 1

4 4 4

1 5 2

Sample Output

2

0

3

РЕШЕНИЕ

структуры данных – дерево Фенвика

Анализ алгоритма

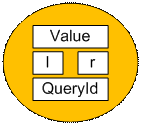
Создадим структуру node с четырьмя полями (значение Value, левая l и правая r границы, номер запроса QueryId) как показано ниже. Заведем массив v таких структур.

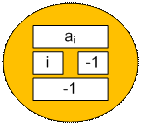
Отсоритуем числа a_i по убыванию, сохранив при этом их позиции в массиве. Эту информацию сохраним в структуре следующим образом:

Перенумеруем запросы начиная с 1 в порядке как они поступают на вход. Запрос номер id, заданный в виде i, j, k сохраним в виде

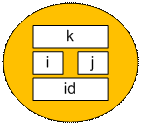
То есть данные о числах a_i и запросах сохранили в массиве структур node. Отсортируем его по убыванию Value. При этом среди элементов с одинаковым значенияем Value сначала должны идти запросы, а потом значения a_i.

Решение задачи при помощи дерева отрезков дает Time Limit.

Построим дерево Фенвика b[0..n], изначально занесем в него нули. Просматриваем массив структур слева направо. Если текущий элемент – число a_i (v[j].r = -1), то увеличим на единицу b[v[j].l]. Если текущий элемент – запрос, то вычисляем сумму элементов массива b с индексами от v[j].l до v[j].r включительно.

Пример

Реализация алгоритма

#include <cstdio>

#include <vector>

#include <cstring>

#include <algorithm>

#define MAX 30010

#define MAXQ 200010

using namespace std;

int Fenwick[MAX], res[MAXQ];

struct node

{

int Value;

int l, r;

int QueryId;

node (int Value, int l, int r = -1, int QueryId = -1) :

Value(Value), l(l), r(r), QueryId(QueryId) {};

int operator< (const node &a) const

{

if (Value == a.Value) return r > a.r;

return Value > a.Value;

}

};

vector<node> v;

int n, q, i, j, l, r, val;

long long Summma0_i(int i)

{

long long result = 0;

for (; i >= 0; i = (i & (i + 1)) - 1)

result += Fenwick[i];

return result;

}

void IncElement(int i, int delta)

{

for (; i <= n; i = (i | (i+1)))

Fenwick[i] += delta;

}

int main(void)

{

scanf("%d",&n);

for(i = 1; i <= n; i++)

{

scanf("%d",&val);

v.push_back(node(val,i));

}

scanf("%d",&q);

for(i = 0; i < q; i++)

{

scanf("%d %d %d",&l,&r,&val);

v.push_back(node(val,l,r,i));

}

sort(v.begin(),v.end());

memset(Fenwick,0,sizeof(Fenwick));

for(i = 0; i < v.size(); i++)

{

if (v[i].r == -1)

IncElement(v[i].l,1);

else

res[v[i].QueryId] = Summma0_i(v[i].r) - Summma0_i(v[i].l - 1);

}

for(i = 0; i < q; i++)

printf("%d\n",res[i]);

return 0;

}