4206. Fast Maximum Matching

FJ has n (1 ≤ n ≤ 50,000) cows and m (1 ≤ m ≤ 50,000) bulls. Given a list of p (1 ≤ p ≤ 150,000) potential matches between a cow and a bull, compute the greatest number of pairs that can be matched. Of course, a cow can be matched to at most one bull, and vice versa.

Input. The first line contains three integers n, m and p. Each of the next p lines contains two integers a (1 ≤ a ≤ n) and b (1 ≤ b ≤ m), denoting that cow a can be matched with bull b.

Output. Print a single integer that is the maximum number of pairs that can be obtained.

Sample input	Sample output
5 4 6 5 2 1 2 4 3 3 1 2 2 4 4	3

РЕШЕНИЕ

графы – максимальное паросочетание

Анализ алгоритма

Для нахождения максимального паросочетания реализуем алгоритм дополняющего пути.

Пример

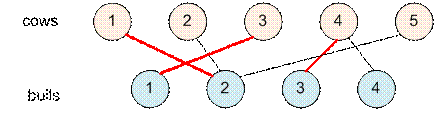
Реализация алгоритма

#include <cstdio>

#include <vector>

using namespace std;

vector<vector<int> > g;

vector<int> used, mt, par;

int i, j, ptr;

int n, m, k, a, b, flow;

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

par[v] = 1;

return 1;

}

}

return 0;

}

void AugmentingPath(void)

{

int i, run;

mt.assign (m+1, -1);

par.assign (n+1, -1);

for (run = 1; run; )

{

run = 0; used.assign(n+1, 0);

for (i = 1; i <= n; i++)

if ((par[i] == -1) && dfs(i)) run = 1;

}

}

int main(void)

{

scanf("%d %d %d",&n,&m,&k);

g.resize(n+1);

for(i = 0; i < k; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

}

AugmentingPath();

for (flow = 0, i = 1; i <= m; i++)

if (mt[i] != -1) flow++;

printf("%d\n",flow);

return 0;

}