5971. LCM Sum
Given n, calculate the sum LCM(1, n) + LCM(2, n) + .. + LCM(n, n), where LCM(i, n) denotes the Least
Common Multiple of the integers i and
n.
Input. The first line
contains the number of test cases t
(1 ≤ t ≤ 300000). Each of
the next t lines contain an integer n (1 ≤ n ≤ 1000000).
Output. Output t lines, one for each test case,
containing the required sum.
|
Sample
Input |
Sample
Output |
|
3 1 2 5 |
1 4 55 |
РЕШЕНИЕ
теория чисел
Анализ алгоритма
Пусть S = 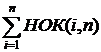 =
= 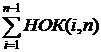 + НОК(n, n)
=
+ НОК(n, n)
= 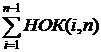 + n, откуда
+ n, откуда
S – n = НОК(1, n) + НОК(2, n) + . . . +
НОК(n – 1, n)
Переставим
слагаемые в правой части в обратном порядке и запишем равенство в виде
S – n = НОК(n – 1, n) + . . . +
НОК(2, n) + НОК(1, n)
Сложим два
равенства:
2(S – n) = (НОК(1, n) + НОК(n – 1, n)) + . . . + (НОК(n – 1,
n)
+ НОК(1, n))
Рассмотрим
выражение в скобках:
НОК(i, n) + НОК(n
– i, n) = 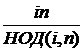 +
+ 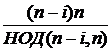
Заметим, что
знаменатели последних двух слагаемых равны: НОД(i, n) = НОД(n – i,
n), следовательно
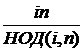 +
+ 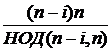 =
= 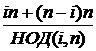 =
=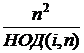
Откуда
2(S – n) = 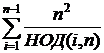 =
= 
НОД(i, n) = d
может принимать только значения делителей числа n, при этом количество i
для которых имеет место указанное равенство, равно φ (n / d). Следовательно
2(S – n) =  =
= 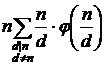 =
= 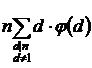 =
= 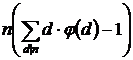
Второе равенство справедливо так как если d делитель n, то n / d также делитель n. При этом если d
≠ n, то n / d ≠ 1.
Последнее равенство справедливо, так как в сумму включили слагаемое 1 * φ
(1) = 1. Осталось выделить из уравнения значение S:
2(S – n) = 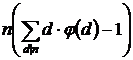 , 2S – 2n =
, 2S – 2n = 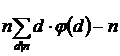 ,
,
S = 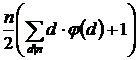
Реализация алгоритма
#include <stdio.h>
#define MAX 1000001
int i, j, n, tests;
long long
res[MAX], phi[MAX], ans;
void FillEuler(void)
{
int i, j;
phi[1] = 1;
for(i = 2; i
< MAX; i++) phi[i] = i;
for(i = 2; i
< MAX; i+=2) phi[i] /= 2;
for(i = 3; i
< MAX; i+=2)
if (phi[i]
== i)
for(j =
i; j < MAX; j += i) phi[j] -= phi[j]/i;
}
int main(void)
{
FillEuler();
for(i = 1; i
< MAX; i++)
for(j = i; j
< MAX; j += i)
res[j] += (i * phi[i]);
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
ans = (res[n] + 1) * n / 2;
printf("%lld\n",ans);
}
return 0;
}