1051. Closest Common Ancestors

Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u, v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)

Input. The data set starts with the tree description, in the form:

nr_of_vertices

vertex:(nr_of_successors) successor1 successor2 ... successorn

......

where vertices are represented as integers from 1 to n. The tree description is followed by a list of pairs of vertices, in the form:

nr_of_pairs

(u v) (x y) ...

The input contents several data sets (at least one).

Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.

Output. For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times

For example, for the following tree:

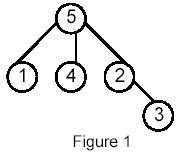
Sample Input

5

5:(3) 1 4 2

1:(0)

4:(0)

2:(1) 3

3:(0)

6

(1,5) (1,4) (4,2)

(2,3)

(1,3) (4,3)

Sample Output

2:1

5:5

РЕШЕНИЕ

LCA

Анализ алгоритма

Для каждого запроса (x y) следует найти LCA(x y) в дереве. Далее следует подсчитать сколько раз каждая вершина будет ответом.

Входные данные содержат несколько тестов. Пробелы, табуляции и переводы строки могут встречаться в любом месте.

Реализация алгоритма

#include <cstdio>

#include <vector>

#include <cstring>

#define MAX 1000

#define LOGMAX 10

using namespace std;

int i, n, q, root, l, x, y, c, lca;

vector<int> g[MAX];

int timer, d[MAX], used[MAX], f[MAX];

int up[MAX][LOGMAX];

char temp[100], ch;

void dfs (int v, int p)

{

int i, to;

d[v] = timer++;

up[v][0] = p;

for(i = 1; i <= l; i++)

up[v][i] = up[up[v][i-1]][i-1];

for(i = 0; i < g[v].size(); i++)

{

to = g[v][i];

if (to != p) dfs (to, v);

}

f[v] = timer++;

}

// if a is a parent of b

int Parent(int a, int b)

{

return (d[a] <= d[b]) && (f[a] >= f[b]);

}

int LCA (int a, int b)

{

if (Parent(a, b)) return a;

if (Parent(b, a)) return b;

for (int i = l; i >= 0; i--)

if (!Parent(up[a][i], b)) a = up[a][i];

return up[a][0];

}

int main(void)

{

while(scanf("%d",&n) == 1)

{

l = 1;

while ((1 << l) <= n) l++;

memset(used,0,sizeof(used));

for(i = 1; i <= n; i++)

g[i].clear();

memset(d,0,sizeof(d));

memset(f,0,sizeof(f));

memset(up,0,sizeof(up));

for(i = 1; i <= n; i++)

{

scanf("%d%[^0-9]",&x, temp);

scanf("%d%[^0-9]",&c, temp);

while(c--)

{

scanf("%d",&y);

g[x].push_back(y);

used[y] = 1;

}

}

for(i = 1; i <= n; i++)

if (!used[i]) root = i;

dfs(root,root);

memset(used,0,sizeof(used));

scanf("%d%[^0-9]",&q,temp);

for(i = 0; i < q; i++)

{

scanf("%d%[^0-9]%d%[^0-9]",&x,temp,&y,temp);

lca = LCA(x, y);

used[lca]++;

}

for(i = 1; i <= n; i++)

if (used[i]) printf("%d:%d\n",i,used[i]);

}

return 0;

}