Матч 303, Отрезки (Segments)

Дивизион 2, Уровень 1

 

На плоскости расположено два отрезка, каждый из которых параллелен или оси абсцисс, или оси ординат. Необходимо определить взаимное расположение отрезков и вернуть:

“NO”, если отрезки не пересекаются

“POINT”, если отрезки имеют общей одну точку

“SEGMENT”, если пересечение отрезков образует сегмент

 

Класс: Segments

Метод: string intersection(vector<int> s1, vector<int> s2)

Ограничения: s1 и s2, содержат по 4 целых числа, каждое из которых находится в промежутке от -1000 до 1000, отрезки параллельны либо оси абсцисс, либо ординат.

 

Вход. Массивы s1 и s2, содержащие координаты концов отрезков. Каждый массив содержит четыре числа x1, y1, x2, y2, формирующие концы отрезка (x1, y1) – (x2, y2).

 

Выход. Одно из слов “NO”, “POINT” или “SEGMENT”  в зависимости от типа взаимного расположения отрезков.

 

Пример входа

s1

s2

{0,0,0,1}

{1,0,1,1}

{0, -1, 0, 1}

{-1, 0, 1, 0}

{10, 0, -10, 0}

{5, 0, -5, 0}

 

Пример выхода

“NO”

“POINT”

“SEGMENT”

 

 

РЕШЕНИЕ

геометрия

 

Построим прямоугольники, ограничивающие отрезки так, чтобы (x1, y1) был его левым нижним концом, а (x2, y2) правым верхним. Для каждого отрезка следует положить

x1 = min(x1, x2), x2 = max(x1, x2), y1 = min(y1, y2), y2 = max(y1, y2)

 

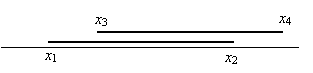Мера пересечения отрезков на прямой. Пусть [x1, x2] и [x3, x4] – два отрезка на прямой (x1 £ x2, x3 £ x4).

 

 

 

 

Пусть left = max(x1, x3) – максимум левых концов, right = min(x2, x4) – минимум правых. Тогда отрезки не пересекаются, если right < left, а в случае пересечения значение right – left будет длиной общей части отрезков.

 

Два отрезка на плоскости, параллельных осям координат, не пересекаются, если не пересекаются их проекции на ось абсцисс или ординат. Два отрезка пересекаются в одной точке, если выполняется условие их пересечения, а мера пересечения их проекций на ось абсцисс и ось ординат равна нулю. Если два отрезка пересекаются, но при этом они имеют более одной общей точки, то их пересечение образует сегмент.

Положим leftx равным максимуму левых концов, rightx минимуму правых, upy минимуму верхних, downy максимуму нижних. Тогда отрезки не пересекаются, если имеет место одно из соотношений:

leftx > rightx или upy < downy

Отрезки пересекаются в одной точке, если

leftx = rightx и upy = downy

Во всех остальных случаях в пересечении отрезки образуют сегмент.

 

ПРОГРАММА

 

#include <cstdio>

#include <vector>

#include <string>

using namespace std;

 

class Segments{

public:

 

  string intersection(vector<int> s1, vector<int> s2)

  {

    int leftx,rightx,upy,downy;

    if (s1[0] > s1[2]) swap(s1[0],s1[2]);

    if (s1[1] > s1[3]) swap(s1[1],s1[3]);

    if (s2[0] > s2[2]) swap(s2[0],s2[2]);

    if (s2[1] > s2[3]) swap(s2[1],s2[3]);

    leftx = max(s1[0],s2[0]);

    rightx = min(s1[2],s2[2]);

    upy = min(s1[3],s2[3]);

    downy = max(s1[1],s2[1]);

    if ((leftx > rightx) || (upy < downy)) return "NO";

    if ((leftx == rightx) && (upy == downy)) return "POINT";

    return "SEGMENT";

  }

};