Матч 458, Произведение троек (ProductTriplet)

Дивизион 2, Уровень 3

 

Заданы шесть целых чисел minx, maxx, miny, maxy, minz и maxz. Вернуть количество троек (x, y, z), которые удовлетворяют следующим условиям:

·        x находится между minx и maxx включительно

·        y находится между miny и maxy включительно

·        z находится между minz и maxz включительно

·        x * y = z

 

Класс: ProductTriplet

Метод: countTriplets(int minx, int maxx, int miny, int maxy,

                     int minz, int maxz)

Ограничения: 1 £ maxx, maxy, maxz £ 109, 1 £ minx £ maxx, 1 £ miny £ maxy, 1 £ minz £ maxz.

 

Вход. Шесть целых чисел minx, maxx, miny, maxy, minz и maxz.

 

Выход. Количество троек (x, y, z), удовлетворяющих выше перечисленным условиям.

 

Пример входа

minx

maxx

miny

maxy

minz

maxz

2

2

3

3

6

6

2

2

3

3

7

7

6

8

4

5

27

35

 

Пример выхода

1

0

4

 

 

РЕШЕНИЕ

математика

 

Рассмотрим частный случай задачи. Пусть значение x0 фиксировано. Вычислим количество троек (x0, y, z), для которых

miny ≤ y ≤ maxy, minz ≤ z ≤ maxz и x0 * y = z

Выведем ограничения на y:

minz ≤ x0 * y ≤ maxz, minz / x0 ≤ y ≤ maxz / x0,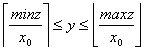

Объединим последнее ограничение y на с miny ≤ y ≤ maxy, получим:

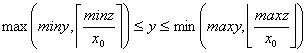
Поскольку любое целое значение y из указанного интервала порождает искомую тройку (x0, y, z), то количество последних при фиксированном x0 равно

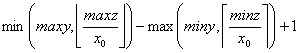
при условии, что указанная разница неотрицательна (иначе интервал y пуст).

Остается перебрать все значения minx ≤ x0 ≤ maxx и подсчитать количество троек для каждого из них. Однако такое решение не пройдет по времени.

Решения уравнения x * y = z будем искать отдельно для каждого из следующих случаев:

·        x = y = ; (1)

·         и таким образом ; (2)

·         и таким образом ; (3)

Тройки решений (x, y, z) во всех трех случаях не пересекаются.

Количество троек, для которых выполняется (1), равно количеству чисел из интервала , не меньших  и не больших .

Для нахождения троек, удовлетворяющих (2), будем следовать выше описанному алгоритму, только перебор по x0 будем делать не только от minx до maxx, а еще и с условием . То есть minx ≤ x0 ≤ min (maxx, ).

Аналогично при нахождении троек, удовлетворяющих (3), будем совершать перебор y0 так, что miny ≤ y0 ≤ min (maxy, ).

 

ПРОГРАММА

 

 

#include <stdio.h>

 

int min(int x, int y)

{

  return (x < y) ? x : y;

}

int max(int x, int y)

{

  return (x > y) ? x : y;

}

 

long long f(long long x0, long long miny, long long maxy,

            long long minz, long long maxz)

{

  // x0 < sqrt(z), x0^2 < z, z >= x0 * x0 + 1

  minz = max(minz, x0 * x0 + 1);

  if (maxz < minz) return 0;

  miny = max(miny, (minz + x0 - 1) / x0);

  maxy = min(maxy, maxz / x0);

  return max(0LL, maxy - miny + 1);

}

 

class ProductTriplet

{

public:

  long long countTriplets(int minx, int maxx, int miny, int maxy,

                          int minz, int maxz)

  {

    long long x0, y0, i, res = 0;

    // x < sqrt(z);

    for(x0 = minx; (x0 <= maxx) && (x0 * x0 < maxz); x0++)

      res += f(x0,miny,maxy,minz,maxz);

    // y < sqrt(z);

    for(y0 = miny; (y0 <= maxy) && (y0 * y0 < maxz); y0++)

      res += f(y0,minx,maxx,minz,maxz);

    for(i = max(minx,miny); (i <= min(maxx,maxy)) && (i * i <= maxz); i++)

      if (minz <= i * i) res ++;

    return res;

  }

};

 

int main(void)

{

  ProductTriplet p;

  //long long res = p.countTriplets(6,8,4,5,27,35);

  //long long res = p.countTriplets(2,2,3,3,7,7);

  long long res = p.countTriplets(8176,184561,1348,43168,45814517,957843164);

  printf("%lld\n",res);

  return 0;

}