Матч 41, Треугольная доска (TrianglesBoard)

Имеется треугольная доска, состоящая из равносторонних треугольников. Треугольники бывают трех типов: “цветные”, “удалить соседей” и “удалить строку”. Треугольники называются соседними, если они имеют общую сторону.

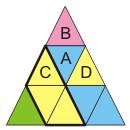
Например, соседними с A являются треугольники B, C, D. Цветные треугольники могут быть покрашены цветом от 0 до 9 включительно. Треугольники остальных типов цвета не имеют. Вы можете выбрать любой треугольник и удалить его. Затем следует рекурсивно удалять треугольники согласно следующим правилам:

1. Если удален цветной треугольник, то далее следует удалить все соседние треугольники того же цвета;

2. Если удален треугольник “удалить соседей”, то далее следует удалить все соседние треугольники независимо от их типа;

3. Если удален треугольник “удалить строку”, то далее следует удалить все треугольники из этой же строки независимо от их типа.

Фраза “рекурсивно удалять” означает, что после удаления очередного треугольника следует проверить его тип, и рекурсивно запустить соответствующую процедуру удаления. Каждый треугольник может быть удален только один раз.

Массив board содержит начальное состояние игры. Треугольники “удалить соседей” обозначаются символом ‘A’, треугольники “удалить строку” – символом ‘R’. Цветные треугольники обозначаются символами от ‘0’ до ‘9’. Вы выбираете начальный треугольник и начинаете с него игру. Счет игры равен числу удаленных цветных треугольников. За удаленные треугольники двух других типов очки не даются. Необходимо найти наибольший счет, который можно получить в игре.

Класс: TrianglesBoard

Метод: int maxScore(vector<string> board)

Ограничения: board содержит от 1 до 50 строк, состоящих из символов ‘A’, ‘R’, ‘0’ – ‘9’, board[i] содержит в точности 2*i+1 элемент.

Вход. Массив строк board, описывающий начальное состояние игры.

Выход. Наибольший счет, который можно получить в игре.

Пример входа

board

{"0",

"121",

"31122"}

{"1",

"121",

"12121"}

{"2",

"122",

"1A122",

"2222222"}

Пример выхода

3

1

12

РЕШЕНИЕ

поиск в глубину

Доску будем хранить в массиве b. Соседями треугольника b[i][j] будут два треугольника этого же ряда b[i][j – 1] и b[i][j + 1], а также или b[i – 1][j – 1] (ячейка верхнего ряда, для нечетного j), или b[i + 1][j + 1] (ячейка нижнего ряда, для четного j). Нумерация рядов сверху вниз и треугольников в ряду слева направо начинается с нуля.

Перебираем все возможные начальные треугольника, для каждого из них запускаем рекурсивную процедуру игры. Для каждой игры подсчитываем ее счет. Наибольший из найденных счетов будет искомым. При каждом запуске игры копируем содержимое массива b в bc. Ячейки массива bc в процессе обработки удаляются, в то время как начальное состояние доски неизменно хранится в массиве b.

Остается реализовать функцию рекурсивного вызова dfs(i, j, ch) – удаление ячейки (i, j) при условии, что в ней удаляется символ ch. Если аргументы i или j выходят за границы массива, или b[i][j] содержит не ch, то возвращаем 0 – ячейка с координатами (i, j) не удалена. Иначе удаляем ячейку, присваивая ей нуль: bc[i][j] = 0. Далее в зависимости от типа ячейки (i, j) совершаем рекурсивное удаление других ячеек согласно описанным в условии правилам. Если текущая ячейка “цветная”, то удаляем соседей ее же цвета, передавая в третьем аргументе рекурсивного вызова dfs символ ch.

ПРОГРАММА

#include <cstdio>

#include <string>

#include <vector>

#include <memory>

using namespace std;

char b[51][102], bc[51][102];

int n;

int dfs(int i,int j,char ch)

{

int s, k;

if (i < 0 || j < 0 || i >= n || j >= 2 * i + 1 || ch == 0 || bc[i][j] != ch) return 0;

bc[i][j] = 0;

if (ch == 'A')

{

if (j % 2) return dfs(i,j-1,bc[i][j-1]) + dfs(i,j+1,bc[i][j+1]) + dfs(i-1,j-1,bc[i-1][j-1]);

else return dfs(i,j-1,bc[i][j-1]) + dfs(i,j+1,bc[i][j+1]) + dfs(i+1,j+1,bc[i+1][j+1]);

}

if (ch == 'R')

{

for(s = k = 0; k < 2 * i + 1; k++) s += dfs(i,k,bc[i][k]);

return s;

}

if (j % 2) return 1 + dfs(i,j-1,ch) + dfs(i,j+1,ch) + dfs(i-1,j-1,ch);

else return 1 + dfs(i,j-1,ch) + dfs(i,j+1,ch) + dfs(i+1,j+1,ch);

}

class TrianglesBoard

{

public:

int maxScore(vector<string> board)

{

int i, j, temp, res = 0;

n = (int)board.size();

for(i = 0; i < n; i++)

for(j = 0; j < 2 * i + 1; j++)

b[i][j] = board[i][j];

for(i = 0; i < n; i++)

for(j = 0; j < 2 * i + 1; j++)

{

memcpy(bc,b,sizeof(b));

temp = dfs(i,j,bc[i][j]);

if (temp > res) res = temp;

}

return res;

}

};