TCO 2003, 4 полуфинал,

Ладейная атака (RookAttack)

Имеется шахматная доска размером rows на cols клеток. Некоторые клетки вырезаны из доски, их координаты заданы в массиве cutouts. Каждая строка cutouts представляет собой список координат вырезанных клеток в формате “r c”, разделенных запятой. Необходимо расположить на оставшейся части доски наибольшее количество ладей, не бьющих друг друга. Две ладьи бьют друг друга, если они находятся на одной горизонтали или вертикали. Вырезанные клетки не являются препятствиями для ладей. Располагать ладью на вырезанной клетке запрещается.

Класс: RookAttack

Метод: int howMany(int rows, int cols, vector<string> cutouts)

Ограничения: 1 £ rows, cols £ 300, cutouts содержит от 0 до 50 строк, каждая из которых содержит координаты клеток, разделенных пробелами. Каждая координата клетки имеет формат “r c” (строка, колонка), 1 £ r £ rows, 1 £ c £ cols.

Вход. Количество строк rows и столбцов cols шахматной доски, а также массив cutouts, содержащий список координат вырезанных клеток.

Выход. Наибольшее количество ладей, которое можно расположить на оставшейся части доски так, чтобы они не били друг друга.

Пример входа

rows	cols	cutouts
8	8	{}
3	3	{"0 0","1 0","1 1","2 0","2 1","2 2"}
3	3	{"0 0","1 2","2 2"}

Пример выхода

8

2

3

РЕШЕНИЕ

максимальное паросочетание

Построим двудольный граф. В первую долю поместим rows вершин, во вторую – cols вершин. Если клетка с координатами (i, j) останется не вырезанной на шахматной доске, то проведем ребро между i - ой вершиной первой доли и j - ой вершиной второй доли. Максимальное паросочетание полученного двудольного графа равно максимальному количеству неатакующих ладей, которое можно разместить на шахматной доске. Задачу решаем при помощи максимального потока, добавив две вершины: исток и сток.

Например, для третьего теста шахматная доска и построенный граф будут иметь вид:

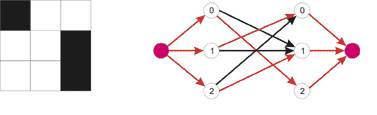
Красным цветом выделены насыщенные ребра в максимальном потоке. Величина потока равна 3, ладьи располагаются в клетках (0, 2), (1, 0) и (2, 1).

При построении матрицы пропускных способностей m вершины графа имеют следующие номера:

· исток: номер 0;

· первая доля: от 1 до rows;

· вторая доля: от rows + 1 до rows + cols;

· сток: номер rows + cols + 1;

ПРОГРАММА

#include <cstdio>

#include <memory>

#include <string>

#include <vector>

#define MAX 602

using namespace std;

int m[MAX][MAX],used[MAX],MaxFlow,flow;

int n;

int aug(int x,int t,int CurFlow)

{

if (x == t) return CurFlow;

if (used[x]++) return 0;

for (int Flow,y = 0; y < n; y++)

{

if (m[x][y] > 0 && (Flow = aug(y,t,min(CurFlow,m[x][y]))))

{

m[x][y] -= Flow; m[y][x] += Flow;

return Flow;

}

}

return 0;

}

class RookAttack

{

public:

int howMany(int rows, int cols, vector<string> cutouts)

{

int i,j,r,c,pos;

string s;

memset(m,0,sizeof(m));

n = rows + cols + 2;

for(i=1;i<=rows;i++) m[0][i] = 1;

for(i=1;i<=cols;i++) m[i+rows][n-1] = 1;

for(i=1;i<=rows;i++)

for(j=1;j<=cols;j++)

m[i][j+rows] = 1;

for(i=0;i<cutouts.size();i++)

{

s = cutouts[i];

while(s.size() > 0)

{

sscanf(s.c_str(),"%d %d",&r,&c);

m[r+1][rows+c+1] = 0;

pos = s.find(',');

if (pos > 0) s.erase(0,pos+1); else break;

}

}

MaxFlow = 0;

do

{

memset(used,0,sizeof(used));

} while ((flow = aug(0,n-1,0x7FFFFFFF)) && (MaxFlow += flow));

return MaxFlow;

}

};