10078. Галерея искусств
Галерея имеет вид простого
многоугольника. Точка внутри галереи называется критической, если из нее не
видны все точки галереи.
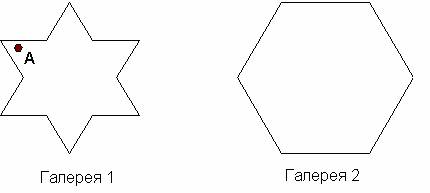
В галерее 1 точка А критическая. Вторая галерея
критических точек не имеет. Необходимо установить, имеет ли заданная галерея
хотя бы одну критическую точку.
Вход. Состоит
из нескольких тестов. Первая строка каждого теста содержит количество вершин n (3 £ n £ 50) многоугольника. Каждая из следующих n строк содержит
координаты вершин (x, y) многоугольника, 0 £ x, y £ 1000. Вершины галереи заданы в порядке ее обхода. Никакие три
последовательные точки не лежат на одной прямой.
Выход. Для каждой галереи вывести
“Yes”, если она содержит критическую точку и “No” иначе.
Пример входа
4
0 0
3 0
3 3
0 3
4
0 0
3 0
1 1
0 3
0
Пример выхода
No
Yes
РЕШЕНИЕ
геометрия
Анализ алгоритма
Галерея не имеет критических
точек, если она имеет вид выпуклого многоугольника. Рассмотрим движение по
границе многоугольника. Если во всех вершинах происходит поворот в одну и ту же
сторону (влево или вправо), то многоугольник выпуклый. Рассмотрим три
последовательные вершины A, B, C. В точке B имеет место левый поворот
(движение происходит против часовой стрелки), если AB ´ BC > 0 и правый, когда AB ´ BC < 0. Для каждой точки Xi+1 с координатами
(xi+1, yi+1) (i = 1, …, n-1, нумерация точек начинается с нуля) следует вычислить значение
векторного произведения и определить направление поворота в ней:
XiXi+1
´ Xi+1Xi+2 = 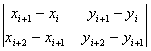
Координаты n входных точек X0, …, Xn-1 хранятся в ячейках массивов с индексами
от 0 до n – 1. Положим Xn = X0, Xn+1 = X1.
При i = n – 1 находится поворот в точке Xn = X0, вычисляется векторное произведение Xn-1Xn ´ XnXn+1 = Xn-1X0 ´ X0X1.
Реализация алгоритма
Координаты вершин многоугольника
храним в массивах x и y. Максимальное количество вершин равно 50. Но в процессе
вычислений необходимо будет держать в массивах на две вершины больше (Xn = X0, Xn+1 = X1).
int x[52],
y[52],
Читаем входные данные. Положим n – ую точку равной нулевой, а n+1
– ую равной первой.
while(scanf("%d",&n),n)
{
for(i = 0;
i < n; i++) scanf("%d %d",&x[i],&y[i]);
x[n] = x[0]; y[n] = y[0];
x[n+1] = x[1]; y[n+1] = y[1];
Вычислим res = X0X1 ´ X1X2, знак
векторного произведения определяет поворот в первой точке.
res = (x[1]-x[0])*(y[2]-y[1]) -
(x[2]-x[1])*(y[1]-y[0]);
Все последующие повороты должны
быть такими же, как и в первой точке. Переменная flag = 0, если все повороты одинаковые. Как только встречается
поворот в другую сторону (temp * res < 0) , устанавливаем flag = 1 и выходим из цикла.
flag = 0;
for(i = 1;
i < n; i++)
{
temp = (x[i+1] - x[i]) * (y[i+2] -
y[i+1]) –
(x[i+2] - x[i+1]) * (y[i+1] -
y[i]);
if (temp
* res < 0) {flag = 1; break;}
}
В зависимости от значения
переменной flag выводим результат.
if (flag)
printf("Yes\n"); else printf("No\n");
}