10213. Сколько частей земли?

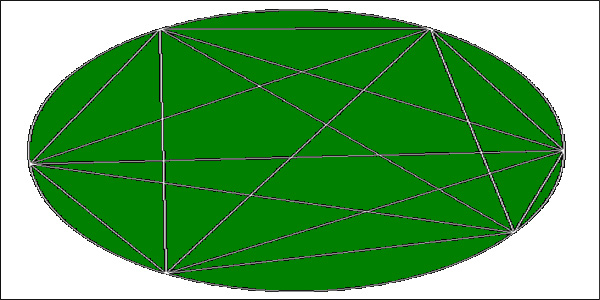
На границе эллипсовидной земли произвольно выбрано n точек. Все пары точек соединены прямыми отрезками. Определить, на какое максимальное количество частей можно таким образом разбить землю. На рисунке ниже приведен пример разбиения земли для n = 6.

Вход. Первая строка содержит количество тестов S (0 < S < 3500). Каждый тест состоит из одной строки и содержит одно число n, (0 £ n £ 2³¹).

Выход. Для каждого теста вывести максимально количество частей, на которое можно разбить землю.

Пример входа

4
1
2
3
4

Пример выхода

1
2
4
8

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Количество областей, на которое поделят хорды эллипс, равно

1 + +

Поскольку n £ 2³¹, а количество областей при максимально возможном значении n, выйдет за пределы 64-битового целочисленного типа, то следует реализовать длинную арифметику.

Реализация алгоритма

Для реализации длинной арифметики воспользуемся классом BigInteger. Во избежание переполнения следует переписать оператор умножения на число.

class BigInteger

{

. . .

BigInteger operator* (long long a)

{

BigInteger Temp(0);

long long i, t, carry = 0;

Temp.len = len;

for(i = 0; i < Temp.len; i++)

{

В этом месте вычисляется произведение числа a на цифру m[i]. Если объявлять переменные a и t типа int, то в произведении a * m[i] возможно переполнение. Чтобы его не случилось, следует объявить переменные a и t 64-битовым целочисленным типом.

t = a * m[i] + carry;

Temp.m[i] = (int)(t % 10);

carry = t / 10;

}

while (carry > 0) {Temp.m[i++] = (int)(carry % 10);

carry /= 10; Temp.len++;}

return Temp;

}

};

Функция Cnk вычисляет биномиальный коэффициент .

BigInteger Cnk(int k, int n)

{

BigInteger res(1);

for(int i = 1; i <= k; i++)

res = res * (n-i+1) / i;

return res;

}

Основная часть программы. Читаем количество тестов tests. Для каждого входного значения n вычисляем результат res по выше приведенной формуле.

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

res = Cnk(2,n) + Cnk(4,n) + 1;

res.print(); printf("\n");

}