10297. Бобер грызун

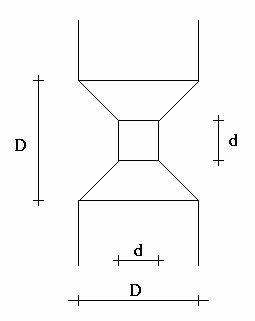
Когда бобер начинает грызть дерево, он из ствола выгрызает весьма специфическую форму. От ствола остается два усеченных конуса, соединенных между собою цилиндром, диаметр которого равен высоте. Задача бобра состоит не в том, чтобы съесть дерево, а в том, чтобы вычислить диаметр соединяющего цилиндра. Помогите ему сделать расчеты.

Рассмотрим идеального бобра, который грызет идеальное дерево. Пусть ствол представляет собой цилиндр диаметром D, и бобер грызет его на отрезке длины D. Чему равен диаметр d внутреннего цилиндра, если бобер сгрыз v кубических единиц древесины?

Вход. Каждая строка содержит два числа D и v. Значение v не превосходит максимального объема, который бобер может выгрызть из дерева. Последняя строка содержит D = 0, v = 0 и не обрабатывается.

Выход. Для каждого теста вывести одно число, округленное до трех десятичных знаков, которое содержит значение d.

Пример входа

10 250

20 2500

25 7000

50 50000

0 0

Пример выхода

8.054

14.775

13.115

30.901

РЕШЕНИЕ

геометрия – бинарный поиск

Анализ алгоритма

Объем цилиндра с радиусом основания r и высотой h равен .

Объем конуса с радиусом основания r и высотой h равен .

Предположим, что значение d известно. Вычислим объем выгрызенной древесины. Для этого следует из объема цилиндра с радиусом основания D / 2 и высотой D вычесть объемы двух оставшихся конусов и маленького цилиндра с радиусом основания d / 2 и высотой d.

Объем цилиндра с радиусом основания D / 2 и высотой D равен =

Объем усеченного конуса равен – = .

Объем маленького цилиндра с радиусом основания d / 2 и высотой d равен

Таким образом, объем выгрызенной древесины равен

vol = – –

Для нахождения диаметра d внутреннего цилиндра воспользуемся бинарным поиском. Очевидно, что чем больше d, тем меньше vol. Изначально 0 ≤ d ≤ D. Положим left = 0, right = D. Пусть d = (left + right) / 2. Вычисляем для этого значения объем выгрызенной древесины vol. Если оно больше заданного v, то нижнюю границу d следует увеличить, положив left = d. Иначе следует уменьшить правую границу, присвоив right = d.

Реализация алгоритма

Читаем входные данные.

while(scanf("%lf %lf",&D,&v), D + v)

{

Инициализируем левую left и правую right границу для значения d (0 ≤ d ≤ D). Запускаем бинарный поиск по d.

left = 0; right = D;

while(right - left > EPS)

{

d = (left + right) / 2;

Если d – текущее значение диаметра внутреннего цилиндра, то объем выгрызенной древесины вычисляем по выше приведенной формуле.

vol = PI*D*D*D/4 - PI*d*d*d/4 - PI/12*(D*D*D - d*d*d);

В зависимости от вычисленного объема сгрызенной древесины изменяем левую или правую границу интервала для значения d. Всегда имеет место неравенство left ≤ d ≤ right.

if (vol > v) left = d; else right = d;

}

Выводим ответ.

printf("%.3lf\n",d);

}