10334. Луч сквозь стекло
Две пластины стекла совместили друг с другом. Сколькими способами an луч света может пройти сквозь пластины, если по пути он изменит направление n раз?
Вход. Каждая строка содержит одно число n (0 £ n £ 1000).
Выход. Для каждого
теста вывести в отдельной строке значение an.
|
Пример
входа |
Пример
выхода |
01
2 |
1 2 3 |
РЕШЕНИЕ
числа
Фибоначчи
Анализ алгоритма
При наложении
двух стеклянных пластин образуется одна внутренняя сторона и две внешние,
относительно которых может отражаться луч света. Каждый проход луча с n
отражениями будем кодировать последовательностью нулей и единиц длины n:
если отражение осуществляется относительно внутренней стороны, то ставим 1,
если относительно внешней – то 0. Например, показанному ниже движению луча с 4
отражениями соответствует последовательность 1, 0, 0, 0.
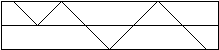
Можно заметить,
что две единицы в такой последовательности никогда не будут стоять вместе,
потому что два последовательных отражения относительно внутренней стороны
никогда не могут иметь место. Таким образом, количество возможных проходов луча
с n отражениями равно количеству последовательностей из 0 и 1 длины n,
в которых две единицы не стоят вместе. Количество таких последовательностей
равно числам Фибоначчи (задача 10450). Числа Фибоначчи имеют вид: f0
= 0, f1 = 1, f2 = 1, fi =
fi-1 + fi-2. Число
способов an прохода луча света сквозь пластины равно fn+2.
Поскольку n
£ 1000, то следует воспользоваться
классом BigInteger.
Пример
Варианты
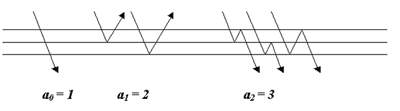
прохождения луча сквозь пластины для n = 0, 1, 2 показаны выше на
рисунке. При этом a0 = f2 = 1, a1
= f3 = 2, a2 = f4 = 3.
Реализация алгоритма
Вычислим все
значения ai (0 £ i £ 1000), занесем их в массив m[1001]. Поскольку a1000
= f1002 содержит не более 210 десятичных знаков, то установим
MAXLENGTH = 210.
#define MAXLENGTH 210
BigInteger
m[1001];
Вычислим все
значения m[i] = ai, 0 £ i £ 1000. Положим m[0] = 1, m[1] = 2, а далее воспользуемся рекуррентной
формулой m[i] = m[i -1] + m[i - 2].
m[0] =
BigInteger(1);m[1] = BigInteger(2);
for(i = 2; i < 1001; i++)
m[i] =
m[i-1] + m[i-2];
Читаем входное
значение n и выводим m[n].
while(scanf("%d",&n)
== 1)
m[n].print();