10450. Шум мирового кубка

По заданному числу n вычислить количество последовательностей из 0 и 1 длины n, в которых две единицы не стоят рядом.

Вход. Первая строка содержит количество тестов. Каждая следующая строка является отдельным тестом и содержит число n (0 < n < 51).

Выход. Для каждого теста вывести его номер и количество последовательностей из 0 и 1 длины n, в которых две единицы не стоят рядом.

Пример входа

2

3

1

Пример выхода

Scenario #1:

5

Scenario #2:

2

РЕШЕНИЕ

числа Фибоначчи

Анализ алгоритма

Обозначим через f(n) количество искомых последовательностей из 0 и 1 длины n. Если на первом месте последовательности будет находиться 0, то начиная со второго места можно построить f(n – 1) последовательностей. Если на первом месте стоит 1, то на втором месте обязательно должен стоять 0, а на последующих n - 2 свободных местах можно построить f(n – 2) последовательностей.

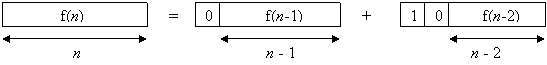
При этом f(1) = 2 (имеем две последовательности длины 2: 0 и 1), f(2) = 3 (последовательности 00, 01, 10). Значения f(n) образуют числа Фибоначчи . Известно, что f₀ = 0, f₁ = 1, f₂ = 1, f_i = f_i-1 + f_i-2. Учитывая начальные условия, получим: f(n) = f_n+2.

Пример

Рассмотрим второй тест. Всего существует 5 последовательностей из 0 и 1 длины 3, в которых две единицы не стоят рядом: 000, 001, 010, 100, 101.

Реализация алгоритма

В массиве fib вычислим значения f(n): f(n) = fib[n]. Для n > 44 значения f(n) будут выходить за границы типа int, поэтому воспользуемся 64 - битовым целочисленным типом long long (в среде Microsoft Visual Studio C++ – тип __int64).

long long fib[51];

Нахождение значений f(n) совершим в цикле:

fib[1] = 2; fib[2] = 3;

for(i=3;i<51;i++) fib[i] = fib[i-1] + fib[i-2];

Читаем количество тестов и для каждого входного n выводим значение fib[n].

scanf("%d",&tests);

for(i=1;i<=tests;i++)

{

scanf("%d",&n);

printf("Scenario #%d:\n",i);

printf("%lld\n\n",fib[n]);

}