10496. Сбор датчиков
Карел
– робот, живущий в прямоугольной системе координат размером не более чем 20 ´ 20.
Карел может двигаться по вертикали и горизонтали, за один ход попадая из точки
(x, y) в одну из соседних (x, y + 1), (x, y
– 1), (x + 1, y), (x – 1, y). В мире Карела
расположено не более 10 датчиков. Роботу необходимо собрать их, совершив
минимальное число передвижений, и при этом вернуться в конце работы на исходную
позицию.
Вход.
Первая строка содержит число тестов. Первая строка каждого теста содержит
размеры координатной системы. Далее следуют два числа, описывающих начальную
позицию Карела. В третьей строке каждого теста находится количество датчиков n,
за которой следуют n строк с координатами датчиков.
Выход. Для каждого теста вывести наименьшее
количество ходов, за которое Карел соберет все датчики и вернется на
первоначальное место.
Пример входа
1
10 10
1 1
4
2 3
5 5
9 4
6 5
Пример выхода
The shortest path has length 24
РЕШЕНИЕ
полный перебор, генерация всех
перестановок
Анализ алгоритма
Поскольку количество n
датчиков не более 10, сгенерируем все возможные перестановки чисел от 1 до n
(их будет не более чем 10! = 3628800). Каждая перестановка будет указывать на
последовательность сбора датчиков. Например, при n = 4 перестановка (4,
3, 1, 2) указывает на то, что сначала следует забрать датчик с номером 4, потом
– с номером 3, затем 1 и 2. Для каждой перестановки (варианта сбора датчиков)
вычисляем число передвижений робота, за которое он эти датчики соберет. Из всех
возможных перестановок выбираем ту, которой соответствует минимальное
количество ходов робота.
Робот может попасть из точки (x1,
y1) в точку (x2, y2)
минимум за |x2 – x1| + |y2
– y1| передвижений.
Пример
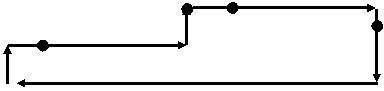
В мире Карела, имеющего размер 10
´ 10, расположено 4 датчика. Начальное положение Карела обозначено буквой
«К», датчики обозначены кругами. Робот может собрать датчики минимум за 24
хода. Путь сбора показан жирной линией: (1, 1) – (1, 3) – (5, 3) – (5, 5) – (9,
5) – (9, 1) – (1, 1). Если датчики перенумеровать в том порядке, в котором они
даны в примере (первый датчик имеет координаты (2, 3), четвертый – (6, 5)), то
оптимальной последовательности их сбора соответствует перестановка (1, 2, 4,
3).
|
10 |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
К |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Реализация алгоритма
Координаты датчиков будем хранить
в массивах x и y (x[i] , y[i] –
координаты i-го датчика). В переменной beepers содержится число
датчиков. В массиве m будем генерировать перестановки чисел от 1 до beepers.
int beepers;
int x[11], y[11], m[10];
Читаем число
тестов. Для каждого теста читаем размер поля (он не существенен в дальнейшей
работе, поэтому отдельных переменных для его хранения не заводим). Начальное
положение Карела заносим в (x[0] , y[0]). Читаем координаты
датчиков, заносим в массив m начальную перестановку (1, 2, …, beepers).
Поскольку робот должен вернуться на исходную позицию, то положим (x[beepers+1]
, y[beepers+1]) = (x[0] , y[0]).
scanf("%d",&tests);
for(t = 0; t < tests; t++)
{
scanf("%d
%d",&x[0],&y[0]);
scanf("%d
%d",&x[0],&y[0]);
scanf("%d",&beepers);
memset(m,0,sizeof(m));
for(i = 1; i
<= beepers; i++)
{
scanf("%d
%d",&x[i],&y[i]);
m[i] = i;
}
x[beepers+1] = x[0]; y[beepers+1] = y[0];
Переменная total будет
содержать минимальное число ходов, за которое можно собрать все датчики.
Генерируем все перестановки чисел от 1 до beepers начиная с
лексикографически наименьшей в ячейках от m[1] до m[beepers] при помощи
функции next_permutation. Для каждой перестановки вычисляем число ходов
необходимое для сбора датчиков в переменной res и изменяем при
необходимости значение переменной total.
total = 2000000000L;
do{
res = 0;
for(i = 1;
i <= beepers + 1; i++)
res
+= abs(x[m[i]] - x[m[i-1]]) + abs(y[m[i]] - y[m[i-1]]);
if (res
< total) total = res;
} while(next_permutation(m+1,m+beepers+1));
Выводим результат.
printf("The
shortest path has length %d\n",total);
}