10497. Любимый ребенок мешает
Ребенок взял у
родителей n вещей, а потом положил их обратно. При этом ни одна вещь не
оказалась на своем месте. Сколькими вариантами ребенок может это сделать?
Вход.
Каждая строка содержит положительное число n (n £ 800) – количество
вещей, которое взял ребенок у родителей. Признак конца входных данных n
= -1.
Выход. Для каждого n вывести
количество способов, которыми ребенок может вернуть все вещи обратно. При этом
ни одна вещь не должна быть возвращена на свое место.
Пример входа
2
3
4
-1
Пример выхода
1
2
9
РЕШЕНИЕ
комбинаторика, задача о беспорядках
Анализ алгоритма
Рассмотрим формулу
включения - исключения. Пусть S – некоторое множество, P = {p1,
p2, …, pn} – свойства, которые могут иметь
элементы из S. Обозначим через S(p1 p2 … pn)
количество элементов из S, которые имеют одновременно свойства p1,
p2, …, pn. Тогда количество элементов из S,
которые не имеют ни одного свойства pi, равно
|S| - ![]() +
+ ![]() - … + (-1)k
- … + (-1)k
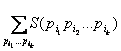 + … + (-1)n
+ … + (-1)n
![]()
Рассмотрим в качестве S множество всех перестановок
чисел от 1 до n. Тогда pi – это свойство перестановки
оставлять на месте элемент i. Беспорядком называется такая перестановка,
в которой не существует ни одного свойства pi.
Таким образом S(![]() ) = (n – k)!, а количество перестановок чисел
от 1 до n, которые оставляют k элементов на месте, равно
) = (n – k)!, а количество перестановок чисел
от 1 до n, которые оставляют k элементов на месте, равно ![]() . Отсюда следует, что количество перестановок - беспорядков
равно
. Отсюда следует, что количество перестановок - беспорядков
равно
n! - ![]() (n - 1)! +
(n - 1)! + ![]() (n - 2)! + … + (-1)k
(n - 2)! + … + (-1)k ![]() (n - k)! + … (-1)n =
(n - k)! + … (-1)n =
n! (1 - 1 + ![]() -
- ![]() + … +
+ … + ![]() + … +
+ … + ![]() )
) ![]()
![]()
Пример. Пусть имеется n =
3 элемента. Тогда количество перестановок, у которых на первом месте стоит 1,
равно 2: это перестановки (1, 2, 3) и (1, 3, 2). Количество перестановок, у
которых на втором месте стоит 2, равно 2: это перестановки (1, 2, 3) и (3, 2,
1). Тройка на третьем месте стоит в перестановках (1, 2, 3) и (2, 1, 3). Таким
образом, S(p1) = S(p2) = S(p3) = 2.
Перестановкой, в которой на
первом месте стоит 1, а на втором 2, является (1, 2, 3). То есть S(p1p2) = 1. Аналогично S(p2p3) = S(p1p3) = 1. Заметим, что S(p1p2 p3) = 1. Таким образом, для трех вещей
количество перестановок – беспорядков равно
3! – 2 – 2 – 2 + 1 + 1 + 1 – 1 = 2
Этими двумя беспорядками будут
перестановки (2, 3, 1) и (3, 1, 2).
Теорема. Обозначим через f(n)
количество перестановок – беспорядков для множества {1, 2, …, n}. Тогда
имеет место рекуррентное соотношение (1):
f(2n) = 2n * f(2n
– 1) + 1,
f(2n + 1) = (2n +
1) * f(2n) – 1,
f(1) = 0
Доказательство. Для четного аргумента имеем:
f(2n) = (2n)! (1 –
1 + ![]() –
– ![]() + … +
+ … + ![]() ) = (2n)! (1 – 1 +
) = (2n)! (1 – 1 + ![]() –
– ![]() + … –
+ … – ![]() ) + 1 =
) + 1 =
(2n) ((2n – 1)! (1 –
1 + ![]() –
– ![]() + … –
+ … – ![]() )) + 1 = (2n) f(2n – 1) + 1.
)) + 1 = (2n) f(2n – 1) + 1.
Аналогично получаем для нечетного
аргумента:
f(2n + 1) = (2n +
1)! (1 – 1 + ![]() –
– ![]() + … –
+ … – ![]() ) =
) =
(2n +1)! (1 – 1 + ![]() –
– ![]() + … +
+ … + ![]() ) – 1 =
) – 1 =
(2n + 1) ((2n)! (1 –
1 + ![]() –
– ![]() + … +
+ … + ![]() )) – 1 = (2n + 1) f(2n) – 1.
)) – 1 = (2n + 1) f(2n) – 1.
Задача решается вычислением всех
значений f(n) для n £ 800.
Второе решение
Выберем число, которое будет
стоять на 1-ой позиции. Это может быть любое число, кроме единицы (имеем (n-1)
вариантов для первого числа). Пусть число, которое стоит на первой позиции,
равно k. Рассмотрим число, которое будет стоять на k-й позиции.
Есть два варианта:
а) Если на k-й позиции
стоит 1, то поменяли числа 1 и k местами, и оставшиеся (n-2)
числа необходимо расставить на оставшиеся (n-2) позиции, то есть задача
сведена к подзадаче для (n-2) чисел, так как удалили два числа вместе с
соответствующими позициями.
б) Допустим, что на k-й
позиции стоит не 1, а какое-то другое число. Рассмотрим подзадачу, в которой
расставим на позиции со 2-й по n-ую числа 1, 2, ... k-1, k+1,
..., n, то есть все числа кроме k, причем число 1 стоит не на
позиции k. Эта подзадача не аналогична исходной, т.к. множество номеров
позиций не совпадает с множеством чисел, которые мы расставляем. Но мы можем в
этой подзадаче заменить число 1 на число k, и при этом условие задачи не
нарушится, потому что знаем, что число 1 не стоит на k-й позиции, как
было оговорено раньше. Таким образом, если заменить в этой подзадаче число 1 на
число k, то получаем исходную задачу, но для (n-1) чисел. Мы
имеем право сделать такую замену, т.к. в этой подзадаче не было 1-й позиции
(т.е. после замены не появятся новые варианты перестановки), и заменяемое число
не стояло на k-й позиции ни в одной из перестановок (то есть замена не
приведет к тому, что некоторые перестановки перестанут удовлетворять условию
задачи).
Пусть ответом задачи будет f(n).
Есть (n-1) вариантов выбора числа для 1-й позиции. Пусть это число k.
Если число 1 стоит на k-й позиции, то оставшиеся числа можно расставить
f(n-2) способами. Если число 1 стоит не на k-й позиции, то
количество расстановок чисел {1, 2, ..., k-1, k+1, ..., n}
на позициях 2...n будет равняться f(n-1). Таким образом, имеем
рекуррентность (2):
f(n) = (n-1) * (f(n-1)
+ f(n-2)),
f(1) = 0, f(2) = 1
Пример
Вычислим значения f(n) используя
формулу и рекуррентное соотношение.
|
рекуррентность (1) |
формула |
|
f(2) = 2 * f(1) + 1 = 1 |
f(2) = 2! (1 – 1 + |
|
f(3) = 3 * f(2) – 1 = 3 – 1 = 2 |
f(3) = 3! (1 – 1 + |
|
f(4) = 4 * f(3) + 1 = 8 + 1 = 9 |
f(4) = 4! (1 – 1 + |
|
рекуррентность (2) |
|
f(3) = 2 * ( f(1) + f(2)) = 2 *
(0 + 1) = 2 |
|
f(4) = 3 * ( f(2) + f(3)) = 3 *
(1 + 2) = 9 |
|
f(5) = 4 * ( f(3) + f(4)) = 4 *
(2 + 9) = 44 |
Реализация алгоритма
В массиве p[801][MAX], MAX = 2000
будем хранить значения f(n) (p[n] = f(n)). pt[i]
будет содержать количество цифр в числе f(i),
m – рабочий массив.
#define MAX 2000
int ptr, n, i, m[MAX];
int p[801][MAX], pt[MAX];
Функция mult(int n) будет
пересчитывать значение f(n) в соответствии с приведенным выше
рекуррентным соотношением (1).
void mult(int
n)
{
int i, carry,
temp;
int res[MAX];
carry = 0;
for(i = 0; i
<= ptr; i++)
{
temp = (carry+m[i]*n);
res[i] = temp % 10;
carry = temp / 10;
}
while(carry
> 0)
{
res[++ptr] = carry % 10;
carry /= 10;
}
memcpy(m,res,sizeof(res));
if (n % 2)
{
i = 0; while(!m[i])
{m[i] = 9; i++;}; m[i]--;
} else
{
i = 0; while(m[i]
== 9) {m[i] = 0; i++;}; m[i]++;
}
}
Основная часть программы. Для каждого
i (2 £ i £ 800) вычисляем значение f(i)
в массиве m и сохраняем его в ячейке p[i].
memset(m,0,sizeof(m)); ptr = 0;
for(i = 2; i <= 800; i++)
{
mult(i);
memcpy(p[i],m,sizeof(m));
pt[i] = ptr;
}
Для каждого входного значения n
выводим содержимое p[n].
while (scanf("%d",&n),n!=-1)
{
if (n == 1)
printf("0"); else
for(i =
pt[n]; i >= 0; i--) printf("%d",p[n][i]);printf("\n");
}