10918. 3 - Разбиение

Сколькими способами можно разбить прямоугольник 3*n косточками домино размера 2*1? Например, прямоугольник 3*12 можно разбить следующим образом:

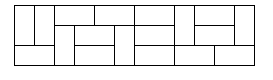
Вход. Каждая строка содержит число n (0 £ n £ 30). Последняя строка содержит n = -1 и не обрабатывается.

Выход. Для каждого значения n вывести количество разбиений прямоугольника 3*n косточками домино размера 2*1.

Пример входа

2

8

12

-1

Пример выхода

3

153

2131

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Обозначим через U_n общее число покрытий 3*n прямоугольника, не разделяя случаев горизонтальных и вертикальных домино. Пусть V_n – число покрытий 3*n прямоугольника без угла с использованием (3n – 1)/2 костяшек домино.

Получим следующие рекуррентные соотношения:

U₀ = 1, U₁ = 0, U_n = 2V_n-1 + U_n-2

V₀ = 0, V₁ = 1, V_n = U_n-1 + V_n-2

Пример

Значения U_n и V_n для малых n приведем в таблице:

n	0	1	2	3	4	5	6	7	8
Un	1	0	3	0	11	0	41	0	153
Vn	0	1	0	4	0	15	0	56	0

Реализация алгоритма

В массивах u и v будем вычислять значения U_n и V_n.

int u[31], v[31];

Вычисляем значения U_n и V_n (n = 0, 1, …, 30) согласно приведенным выше рекуррентным формулам.

u[0] = v[1] = 1;

u[1] = v[0] = 0;

for(n = 2; n <= 30; n++)

{

u[n] = 2 * v[n-1] + u[n-2];

v[n] = u[n-1] + v[n-2];

}

Для каждого входного значения n выводим u[n].

while(scanf("%d",&n),n >= 0)

printf("%d\n",u[n]);