10994. Простое сложение

Определим рекурсивную функцию f(n) следующим образом:

f(n) =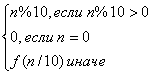

Определим функцию S(p, q) следующим образом:

S(p, q) =

В задаче необходимо вычислить значение S(p, q) по заданным p и q.

Вход. Каждая строка содержит два неотрицательных 32-битовых знаковых числа p и q (p £ q). Последняя строка содержит два отрицательных целых числа и не обрабатывается.

Выход. Для каждой пары p и q вывести значение S(p, q).

Пример входа

1 10

10 20

30 40

-1 -1

Пример выхода

46

48

52

РЕШЕНИЕ

рекуррентное соотношение

Анализ алгоритма

Приведенная в условии функция f(n) находит последнюю ненулевую цифру числа n. Обозначим через

g(p) =

Тогда S(p, q) = g(q) – q(p – 1). Для вычисления функции g(p), суммы последних значащих цифр для чисел от 1 до p, разобьем числа от 1 до p на три множества (операция деления ‘/’ является целочисленной):

1. Числа от (p/10)*10 + 1 до p;

2. Числа от 1 до (p/10)*10, не оканчивающиеся нулем;

3. Числа от 1 до (p/10)*10, оканчивающиеся нулем;

Например, при p = 32 к первому множеству отнесутся числа 31, 32, ко второму 1, …, 9, 11, …, 19, 21, …, 29, к третьему 10, 20.

Сумма последних значащих цифр в первом множестве равна 1 + 2 + … + p%10 = t(1 + t) / 2, где t = p % 10. Во втором множестве искомая сумма равна p / 10 * 45, так как сумма всех цифр от 1 до 9 равна 45, а число полных десятков равно p / 10. Требуемую сумму для третьего множества найдем рекурсивно: она равна g(p / 10).

Реализация алгоритма

Поскольку выполняется обработка 32-битовых знаковых чисел, то во избежании переполнения, при вычислениях используем тип long long.

long long p, q;

Функция g(p) вычисляет сумму значений функции f(n) для значений аргумента n от 1 до p.

long long g(long long p)

{

long long t = p % 10;

if (!p) return 0;

return t * (1 + t) / 2 + p / 10 * 45 + g(p / 10);

}

Значение функции S(p, q) считаем как g(q) – q(p – 1).

long long s(long long p, long long q)

{

return g(q) - g(p - 1);

}

Основной цикл программы. Для каждой пары чисел p и q выводим значение s(p, q).

while(scanf("%lld %lld",&p,&q), p + q >= 0)

printf("%lld\n",s(p,q));