10519. Действительно странно
На
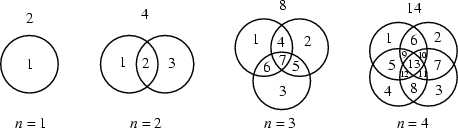
какое максимальное количество частей могут разбить плоскость n окружностей?
Вход.
Каждая строка содержит целое неотрицательное n – число окружностей.
Выход. Для
каждого теста вывести количество частей, на которое могут разбить плоскость n окружностей.
Пример входа
34
Пример выхода
8
14
РЕШЕНИЕ
длинная арифметика + комбинаторика
Анализ алгоритма
Пусть n окружностей
разбивают плоскость на f(n) частей. Одна окружность разбивает плоскость
на 2 части. Каждая следующая n - ая окружность должна иметь максимально
возможное количество пересечений с каждой из (n – 1) предыдущих
окружностей. Две окружности могут пересекаться максимум в двух точках. Поэтому
f(n) = f(n – 1) + 2
* (n – 1),
f(1) = 2
Решим рекуррентное уравнение:
f(n) = 2 * ((n – 1)
+ (n – 2) + … + 1) + 2 == 2 * ![]() + 2 = n * (n
– 1) + 2
+ 2 = n * (n
– 1) + 2
Заметим, что f(0) = 1, так как
ноль фигур делят плоскость на одну часть.
В задаче необходимо реализовать
длинную арифметику, следует воспользоваться классом BigInteger.
Реализация алгоритма
Положим длину чисел MAXLENGTH
равной 1001. Входное число читаем в массив
s.
#define MAXLENGTH 1001
char s[MAXLENGTH];
Строковое представление числа
преобразовываем в тип BigInteger и присваиваем переменной n. Вычисляем результат по формуле n * (n – 1) + 2 и выводим
его. Отдельно обрабатываем случай, когда n = 0.
while(gets(s))
{
n = BigInteger(s);
if (n ==
BigInteger("0")) printf("1\n");
else (n * (n
- 1) + 2).print();
}