10542. Гипер - устройство
Пусть P и Q – точки в n мерном пространстве, координаты
которых соответственно равны P(p1, p2, …, pn)
и Q(q1, q2,
…, qn). Все
пространство поделено на n - мерные
гиперкубы. Например, рассмотрим пространство 5 * 4 * 3, состоящее из 60 кубиков
1 * 1 * 1.
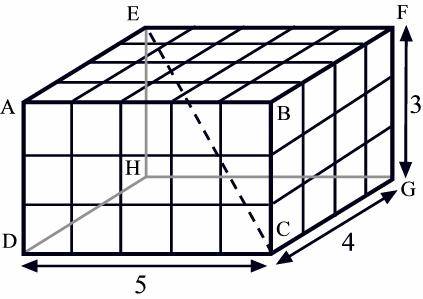
Точки P и Q соединены отрезком.
Через какое количество кубиков проходит этот отрезок?
Вход. Первая
строка содержит количество тестов n (n £ 501). Каждый тест начинается с
числа dim (0 £ dim £ 10) – размерности пространства. Каждая из следующих строк содержит по d чисел, которые являются координатами
точек P и Q. Все координаты положительны и не более 32-битового знакового
целого числа.
Выход. Для каждого теста вывести в
отдельной строке его номер и количество кубиков, через которое проходит отрезок
PQ.
Пример входа
2
2
10 10
10 13
1
10
20
Пример выхода
Case 1: 0
Case 2: 10
РЕШЕНИЕ
комбинаторика, принцип
включения – исключения, НОД
Анализ алгоритма
Построим вектор d = (|p1 – q1|,
|p2 – q2|, …, |pn
– qn|) = (d1, d2, …, dn).
Ответ res можно вычислить, используя
формулу включения - исключения.
Если d = (d1, d2), то res = d1 + d2 – gcd(d1, d2).
Если d = (d1, d2, d3), то res =
d1 + d2 + d3 – gcd(d1, d2)
– gcd(d1, d3) – gcd(d2, d3) + gcd(d1,
d2, d3).
Реализация алгоритма
Считываем входные данные для каждого теста.
scanf("%lld",&n);
for(test = 0; test < n; test++)
{
scanf("%lld",&dim);
for(i = 0; i
< dim; i++) scanf("%lld",&a[i]);
for(i = 0; i
< dim; i++) scanf("%lld",&b[i]);
Вычисляем массив d
= (|p1 – q1|, |p2 – q2|,
…, |pn – qn|) = (d1, d2,
…, dn).
for(i = 0; i
< dim; i++) d[i] = (a[i] > b[i]) ? a[i] - b[i] : b[i] - a[i];
res = 0;
Перебираем все подмножества множества {d1, d2, …, dn}. Каждое
подмножество генерируется по числу i
(1 £ i
£ 2dim
– 1), выбирая из его двоичного представления позиции, на которых стоят единицы.
for(i = 1; i
< 1<<dim; i++)
{
ptr = temp = cnt = 0; j = i;
while(j
> 0)
{
if (j %
2)
{
temp = gcd(temp,d[ptr]);
cnt++;
}
ptr++; j /= 2;
}
Если подмножество состоит из четного количества элементов,
то НОД его элементов вычитается их общего результата. Если из нечетного – то
прибавляется.
res += (cnt % 2) ? temp : -temp;
}
Выводим результат
printf("Case
%lld: %lld\n",test+1,res);
}