10543. Путешествующий политик
Политику необходимо провести не менее
k публичных выступлений. В один день
может быть произнесено не более одной речи. Если политик желает провести
несколько выступлений в одном и том же городе, то они не должны проводиться в
соседние дни, так как это будет не эффективно. Однако выступать в одном и том
же городе хотя бы через день уже эффективно.
Первая речь должна быть проведена
политиком в его родном городе, последняя – в столице. Какое наименьшее
количество выступлений необходимо провести политику, чтобы их
последовательность удовлетворяла всем выше перечисленным требованиям?
Вход. Состоит
из нескольких тестов. Первая строка каждого теста содержит три числа – n (количество городов, 2 £ n £ 50), m (количество дорог) и k (минимальное количество выступлений,
2 £ k £ 16). Следующие m строк содержат пару чисел u
и v, означающих возможность посещения
города v после u. Родной город политика имеет номер 0, столица имеет номер n – 1. Последний тест содержит три нуля
и не обрабатывается.
Выход. Для каждого теста вывести наименьшее
возможное количество выступлений. Если это совершить невозможно, то вывести
“LOSER”. Если требуемое количество выступлений будет больше 20, то вывести
также “LOSER”.
Пример входа
3 3 3
0 1
0 2
1 2
5 6 5
0 1
0 3
1 2
2 4
3 2
3 4
3 3 10
0 1
1 0
1 2
0 0 0
Пример выхода
3
LOSER
11
РЕШЕНИЕ
графы, количество путей
между вершинами
Анализ алгоритма
Поскольку
по условию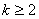 
, то политику следует совершить хотя бы один переход из
одного города в другой. Если политик совершит в точности 
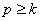выступлений, то ему
необходимо будет p – 1 раз переходить
из одного города в другой (длина пути политика равна p – 1).
Теорема. Пусть А – матрица смежности графа.
Тогда Ak[i][j]
содержит количество путей из i - ой
вершины в j - ую, длины которых в
точности равны k.
Задача состоит в том, чтобы найти
наименьшее (p < 21), для которого значение
Ap–1[0][n – 1] будет не нулевым (0 – начальный город, (n – 1) – последний город, столица).
Пример
Карта страны для третьего теста
имеет вид:
Чтобы
совершить как минимум 10 выступлений, начиная в городе 0 и заканчивая в 2,
необходимо сделать 11 следующих выступлений: 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 2.
Реализация алгоритма
Матрицу смежности графа храним в
массиве mas. Массив temp будет использоваться при умножении матриц.
int mas[50][50], temp[50][50];
Читаем
данные текущего теста. Заполняем матрицу смежности mas.
while(scanf("%d
%d %d",&n,&m,&k),n + m + k)
{
memset(mas,0,sizeof(mas));
for(i = 0; i
< m; i++)
{
scanf("%d
%d",&a,&b);
mas[a][b] = 1;
}
Скопируем данные массива mas в
temp. Далее в temp будет храниться начальное состояние массива mas. В то время
как массив mas будет последовательно хранить temp, temp2, temp3,
и так далее.
memcpy(temp,mas,sizeof(mas));
Вычисляем mas = tempk
– 1 (для этого следует осуществить k
– 2 матричных умножений).
for(i = 1; i
< k - 1; i++) mult();
Пока k < 21
(количество выступлений не более 20) и мы еще не дошли до n – 1 - го города (столицы), совершаем еще одно выступление,
увеличивая k на 1 и соответственно
пересчитывая mas = mas * temp при помощи функции mult.
while ((k
< 21) && (!mas[0][n-1]))
{
mult(); k++;
}
Выводим ответ согласно условию
задачи.
if (k == 21)
printf("LOSER\n");
else
printf("%d\n",k);
Функция
mult совершает умножение mas = mas * temp
void mult(void)
{
int i, j, k,
s;
int
m1[50][50];
for(i = 0; i
< n; i++)
for(j = 0; j
< n; j++)
{
s = 0;
for(k = 0;
k < n; k++)
s += mas[i][k] * temp[k][j];
m1[i][j] = s;
}
memcpy(mas,m1,sizeof(m1));
}