10546. Гнездо
Орла
"Гнездо орла"
представляет собой приключенческую игру. Основной смысл игры состоит в
уничтожении хороших парней, создании общественного порядка, сборе денег с
незаконной деятельности, постепенно превращаясь в успешного гангстера. Но быть
гангстером не так просто в этой игре.
Игра имеет нелинейную сюжетную линию,
которая позволяет игроку выбирать одну из нескольких альтернативных миссий.
Однако здесь есть одна ловушка. Игрок каждый раз может выбирать миссии,
сложность которых больше чем любая из предыдущих законченных. И когда миссия
закончена, она больше не доступна игроку. Единственное исключение составляют
первая и последняя миссии, которые никогда не удаляются и даже не представлены
в списке возможных миссий. Как Вы уже догадались, это соответственно самая
легкая и самая трудная миссии. Очевидно, что игру можно закончить, не сыграв
много миссий. Именно поэтому разработчики игры предложили некоторые бонусы тем,
кто сможет сыграть наибольшее количество миссий. И поверьте, бонусы стоят того.
Вы получите больше здоровья, оружия и других вещей для победы!
Для заинтересованных игроков
существуют еще более потрясающие новости. Пусть K – максимальное количество
миссий, которое может быть закончено, когда игрок завершает игру первый раз.
Если кто-то сможет пройти игру несколько раз (начиная с первой миссии и заканчивая
последней) таким образом, что в точности K миссий будет завершено каждый раз за
игру, и при этом будет сыграно наибольшее количество игр при заданных
ограничениях, то игрок получит бесконечное количество оружия и непобедимость. И
это еще не все; все миссии будут открыты для игрока. А это значит, что будут и
бесконечное оружие, бесконечное здоровье, а также бесконечное число хороших
парней в Вашей власти.
Ваша задача проста и очевидна.
Необходимо заинтересованному игроку помочь выбрать максимальное количество
миссий, которое можно закончить при заданных ограничениях. Порядок миссий в
каждой игре важен, он должен строиться согласно сюжетной линии.
Вход. Первая
строка содержит значение N, 2 < N < 100. Каждая из следующих N строк
содержит название миссии и уровень ее сложности. Название миссии содержит до 20
символов, а уровень сложности характеризует положительное целое число. Символы
в названии миссии чувствительны к регистру, и могут содержать только буквы,
числа и символ подчеркивания. Уровень сложности не более 108. Название миссии в
каждом тесте не дублируется.
Выход. Вывести максимальное количество
миссий, которое может быть завершено при заданных ограничениях. Это число
должно не включать в себя первую и последнюю миссию.
Пример входа
3
Rob_The_Cop
6
A_Petty_Thief
5
Meet_The_Boss
3
3
Meet_The_Boss
3
Rob_The_Cop
6
A_Petty_Thief
5
5
a1
4
a2
2
a3
7
a4
3
a5
1
0
Пример выхода
Case
#1: 3
Case
#2: 2
Case
#3: 4
РЕШЕНИЕ
наибольшая возрастающая
подпоследовательность + потоки
Анализ алгоритма
Пусть К равно длине наибольшей возрастающей подпоследовательности (НВП),
составленной из уровней сложности. Именно столько миссий будет завершено
игроком в первой игре. Вычисляем
это значение К. При этом для каждого элемента
входной последовательности фиксируем, на каком месте НВП он может находиться.
Дальше строим многоярусную сеть (multistage
network). В один ярус включаются те элементы, которые могут находиться на одном
и том же месте НВП. Каждому элементу ставим в соответствие две вершины графа,
соединенные ребром как показано ниже в примере. Ребра ведут только от элементов
одного яруса к строго меньшим элементам соседнего левого яруса. Вводим две
дополнительные вершины: исток и сток. Из истока ребра идут в вершины,
соответствующие элементам, которые могут находиться на К - ом месте НВП, а из
элементов, которые могут находиться на первом месте НВП, идут ребра в сток. Все
ребра ориентированные, их пропускная способность равна 1.
Ответом задачи будет величина максимального
потока построенной сети, умноженная на длину НВП (число К).
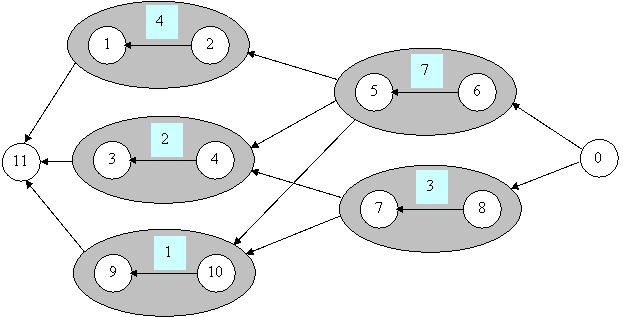
Пример
Построим граф, соответствующий
третьему тесту