10678. Смотрящая корова

В поле пасется корова. На шее у нее имеется кольцо, сквозь которое продета веревка. Концы веревки привязаны к двум кольям, вбитым в землю. Веревка может свободно скользить по кольцу. Известны длина веревки и расстояние между кольями. Необходимо вычислить площадь травы, которую может общипать корова.

Вход. Первая строка содержит количество тестов n (n £ 100). Каждая следующая строка содержит расстояние между кольями d (0 £ d £ 1000) и длину веревки l (d < l £ 1500).

Выход. Для каждого теста вывести площадь травы, которую может общипать корова. Площадь выводить с тремя знаками после запятой.

Пример входа

3

10 12

23 45

12 18

Пример выхода

62.517

1366.999

189.670

РЕШЕНИЕ

геометрия

Анализ алгоритма

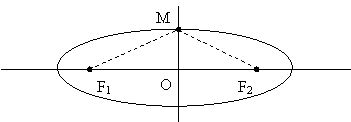
Область травы, доступной для еды, образует внутреннюю область эллипса. Вбитые колья являются фокусами F₁ и F₂. Исходя из определения эллипса, длина большей полуоси равна a = l / 2. В треугольнике OMF₂ известны OF₂ = d / 2, MF₂ = l / 2. Отсюда b = OM = / 2. Площадь эллипса (площадь травы, которую может съесть корова), равна pab.

Реализация алгоритма

Определим константу p = 2 arccos(0).

double pi = 2 * acos(0);

Вычисляем длины полуосей эллипса a и b. Находим и печатаем площадь S = pab.

scanf("%d",&n);

for(i = 0; i < n; i++)

{

scanf("%lf %lf",&d,&l);

a = l / 2;

b = sqrt(l*l - d*d)/2;

s = pi * a * b;

printf("%.3lf\n",s);

}