10681. Путешествие Теобальдо
Теобальдо
необходимо совершить переход из города s в город e, затратив на
него не более чем d дней. Так как Теобальдо ленивый, он хочет потратить
на путешествие максимально возможное число дней. Каждый следующий день
Теобальдо должен переходить из одного города в другой. В задаче требуется
узнать, сможет ли Теобальдо выполнить переход.
Вход.
Состоит из нескольких тестов. Первая строка каждого теста содержит количество
городов c (0 < c £ 100) и количество дорог l
(0 £ l £ 500) между городами. Каждая из
следующих l строк содержит номера двух городов A и B (1 £ a,
b £ c, a ¹ b), соединенных дорогой.
Далее следует строка, содержащая номер начального города s, номер
конечного города e и максимальное число дней d (0 £ d
£ 200), отведенное на путешествие. Последний тест содержит c = l
= 0 и не обрабатывается.
Выход. Для каждого теста вывести
сообщение о том, сможет ли Теобальдо совершить переход, в соответствии с ниже
приведенным форматом.
Пример входа
3 2
1 2
2 3
3 1 2
3 2
1 2
1 3
1 3 2
0 0
Пример выхода
Yes, Teobaldo can travel.
No, Teobaldo can not travel.
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Пусть gok[i]
= 1, если Теобальдо может попасть из начального города s в город i
за k переходов, иначе gok[i] = 0. Изначально go0[s]
= 1, go0[i] = 0, 1 £ i £ c,
i ¹ s. Будем моделировать все возможные переходы Теобальдо, вычисляя значения
gok[i], 1 £ i £ c,
1 £ k £ d. Очевидно, что gok[i]
= 1, если существует такое j, что gok-1[j]
= 1 и существует ребро из города j в город i. Имея все значения
gok[i] (1 £ i £ c)
для некоторого k (0 £ k £ d
– 1), вычисляем все значения gok+1[i], 1 £ i
£ c. Теобальдо может совершить переход из города s в город e
за d дней, если god[e] = 1.
Пример
Рассмотрим данные первого
теста. Теобальдо следует перейти из города s = 3 в город e = 1 за
d = 2 дня. Симметрическая матрица переходов m имеет вид:
m = 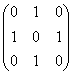
Значения gok[i]
для каждого k - ого перехода приведены в таблице:
|
номер перехода k |
gok[1] |
gok[2] |
gok[3] |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
2 |
1 |
0 |
1 |
Из
третьего города за два дня можно перебраться или в первый город, или снова
вернуться в третий. Поскольку e = 1, d = 2 и god[e]
= go2[1] = 1, то Теобальдо может совершить путешествие.
Реализация алгоритма
Определим максимально возможное
число городов MAX = 101. В массиве m содержим матрицу смежности графа, в
массивах go и go1 будем пересчитывать значения gok[i].
#define MAX 101
int m[MAX][MAX], go[MAX], go1[MAX];
Для каждого теста читаем значения
c и l, обнуляем используемые массивы.
while (scanf("%d
%d",&c,&l), c + l > 0)
{
memset(m,0,sizeof(m));
memset(go,0,sizeof(go));
memset(go1,0,sizeof(go1));
Читаем
информацию о дорогах между городами, строим матрицу смежности. Дороги двусторонние.
for(i = 0; i
< l; i++)
{
scanf("%d %d",&a,&b);
m[a][b] = m[b][a] = 1;
}
Вводим данные о маршруте
Теобальдо, устанавливаем go[s] = 1.
scanf("%d %d
%d",&s,&e,&d);
go[s] = 1;
Для каждого k, 1 £ k
£ d, совершаем пересчет значений gok[i].
Считаем, что gok – 1[i] находятся в массиве
go, а gok[i] кладем в массив go1. Затем копируем
массив go1 в массив go и так повторяем процесс d раз.
for(i = 0; i
< d; i++)
{
for(x = 1;
x <= c; x++)
for(y = 1;
y <= c; y++)
if (go[y]
&& m[y][x])
{
go1[x] = 1; break;}
memcpy(go,go1,sizeof(go));
memset(go1,0,sizeof(go1));
}
В зависимости от значения go[e] печатаем результат.
if (go[e])
printf("Yes, Teobaldo can travel.\n");
else
printf("No, Teobaldo can not travel.\n");
}