10684. Джекпот

Известна последовательность целых чисел, которая выдается игровым автоматом. Известно, что игрок может в какой-то момент начать играть и в определенный момент закончить. Выигрышем считается сумма всех чисел, выпавшая во время игры. Необходимо определить величину максимального выигрыша, который может достаться игроку.

Вход. Состоит из нескольких тестов. Первым числом каждого теста является длина последовательности n (n £ 1000), за которой следуют n целых чисел. Входные данные заканчиваются, когда n = 0.

Выход. Для каждого теста вывести максимально возможный выигрыш или сообщение “Losing streak.”, если игрок не сможет выиграть независимо от момента начала и длительности игры.

Пример входа	Пример выхода
5 12 -4 -10 4 9 3 -2 -1 –2 0	The maximum winning streak is 13. Losing streak.

РЕШЕНИЕ

обработка последовательности

Анализ алгоритма

В задаче следует найти такую подпоследовательность подряд идущих чисел, которая будет иметь максимально возможную сумму среди всех возможных таких подпоследовательностей. Если на подпоследовательности x_i, x_i+1, ..., x_j достигается максимальная сумма, то для любого k, 1 £ k < i и l, j < l £ n сумма элементов x_k, ..., x_i-1 и x_j+1, ..., x_l будет отрицательной.

Пусть ищется максимальная сумма на подпоследовательности x_i, x_i+1, ..., x_j. Строим суммы s(l) = 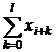, l = 0, 1, …, j – i. Вычисляем в переменной max максимум среди значений s(0), s(1), …, s(t) пока не найдем наименьшее t, для которого s(t) < 0. Если t = j – i (все элементы подпоследовательности просмотрены), то максимальная сумма находится в max. Иначе аналогично ищем максимальную сумму на подпоследовательности x_t+1, x_t+2, ..., x_j с учетом предыдущего максимального значения max. Изначально переменной max присвоим 0. Если в конце алгоритма значение max остается равным 0, то игрок не может выиграть независимо от времени начала и продолжительности игры.

Очевидно, что если в последовательности присутствует хотя бы одно положительное число s, то игрок всегда может выиграть сумму s, начав игру непосредственно перед тем, как автомат выдаст число s и закончив игру сразу же после его выпадения. Фраза “Losing streak.” должна будет быть выведена, если во входной последовательности отсутствуют положительные числа.

Пример

Рассмотрим первый тест. Последовательность состоит из 5 чисел: 12, -4, -10, 4, 9. соответственные значения частичных сумм равны: 12, 8, -2 (здесь текущее значение частичной суммы обнуляем и начинаем отсчет суммы со следующего числа), 4, 13. Максимальное значение среди всех частичных сумма равно 13, что и является максимально возможным выигрышем. Игрок должен начать игру перед тем, как выпадет число 4, и играть до конца генерации последовательности игровым автоматом.

Во втором тесте все числа отрицательные, поэтому игрок проиграет независимо от времени начала и продолжительности игры.

Реализация алгоритма

Читаем длину последовательности n. Обнуляем значение максимального выигрыша max и текущей частичной суммы s.

while (scanf("%d",&n), n > 0)

{

s = 0; max = 0;

Читаем n чисел. Каждое прочитанное число Number добавляем к текущей сумме s и пересчитываем текущее значение выигрыша max. Если на каком-то шаге значение s стало отрицательным, то положим его равным нулю и продолжим процесс.

for(i = 0; i < n; i++)

{

scanf("%d",&Number);

s += Number;

if (s > max) max = s;

if (s < 0) s = 0;

}

Выводим результат в зависимости от значения переменной max.

if (max > 0) printf("The maximum winning streak is %d.\n",max);

else printf("Losing streak.\n");

}