10702. Путешествующий торговец
Джин – путешествующий торговец.
Он ходит по городам, продавая и покупая товары. Страна, по которой он ходит,
состоит из С городов. Начиная свой путь из города S, Джин должен сделать T
переходов между городами. Торговцу разрешается посещать города, в которых он
уже был. Свой путь Джин должен завершить в одном из E городов. Известна
прибыль, которую Джин получает, совершив переход из i - го города в j
- ый. Необходимо вычислить максимальную прибыль, которую он может получить, пройдя
весь путь.
Вход. Состоит из нескольких тестов.
Первая строка каждого теста содержит четыре целых числа: количество городов C
(2 £ С £ 100), номер начального города S
(1 £ S £ 100), число финальных городов E
(1 £ E £ 100) и количество переходов T (1
£ T £ 1000). Следующие С строк
содержат по С чисел. j - ое число i – ой строки содержит прибыль,
которую получит Джин совершив переход из i - го города в j – ый.
Поскольку Джин не может идти из i - ого города в i - ый, то i
- ое число i – ой строки содержит 0. Далее в одной строке следуют E
номеров городов, в которых торговец может завершить свой путь. Последний тест
содержит C = S = E = T = 0 и не обрабатывается.
Выход. Для каждого теста вывести
максимальную прибыль, которую Джин может получить завершив свой путь.
Пример входа
3 1 2 2
0 3 5
5 0 1
9 2 0
2 3
0 0 0 0
Пример выхода
7
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Нумерацию
городов буем начинать с 0 (для удобства программирования на Си). Обозначим
через dk[i] максимальную прибыль, которую может
получить торговец, если после совершения k переходов закончит свой путь
в городе i (0 £ i < C, города нумеруются от 0 до C - 1).
Изначально d0[S] = 0 (нулевая прибыль), d0[i] = -1
(прибыль не определена) для i ¹ S. Массив fin[i] будет
содержать 1, если Джин может завершить свой путь в городе i и 0 иначе.
Матрица m[i, j] (0 £ i, j < C) будет содержать прибыль,
которую можно получить при переходе из города i в j.
Торговец должен совершить T
переходов. Для каждого перехода будем пересчитывать значения d[i]. На k
- ом переходе в i - ый город
можно попасть из j - ого города (0 £ j < C), при этом максимальная прибыль при
достижении i - ого города составит
dk[i] = ![]() (dk-1[j] + m[j, i])
(dk-1[j] + m[j, i])
Условие
dk-1[j]
³ 0 гарантирует, что из начального города S за k - 1
переходов можно добраться до города j.
Для нахождения результата следует
найти максимальное значение среди dT[i], для которых fin[i]
= 1 (город i может быть финальным).
Пример
Рассмотрим тест, данный в условии задачи.
Поскольку нумерацию городов будем вести с нуля, то начальным городом будет 0, а
конечными – 1 или 2. Матрица стоимостей переходов имеет вид:
m = 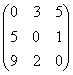
Значения dk[i]
для каждого k - ого перехода приведены в таблице:
|
номер перехода k |
dk[0] |
dk[1] |
dk[2] |
|
0 |
0 |
-1 |
-1 |
|
1 |
0 |
3 |
5 |
|
2 |
14 |
7 |
5 |
Ответом будет max(d2[1], d2[2]) = 7.
Реализация алгоритма
Пока первая строка очередного
теста не содержит четыре нуля, читаем входные данные. Заполняем значения
массивов d, fin, m. При этом помним, что нумерация городов
в тестах начинается с 1, а в массивах будем хранить их с 0.
while(scanf("%d
%d %d %d\n",&c,&s,&e,&t), c + s + e + t > 0)
{
s--;
for(i = 0; i
< c; i++) {d[i] = -1; fin[i] = 0;}
for(d[s] = i
= 0; i < c; i++)
{
for(j = 0;
j < c; j++)
scanf("%d",&m[i][j]);
scanf("\n");
}
for(i = 0; i
< e; i++)
scanf("%d",&j),
fin[j-1] = 1;
scanf("\n\n");
Для каждого из T переходов
динамически пересчитываем оптимальные значения прибыли d[i] по выше
приведенной формуле. Используем вспомогательный массив d1[i] .
while (t >
0)
{
for(i = 0;
i < c;i++)
{
for(d1[i]
= j = 0; j < c; j++)
{
if
(d[j] == -1) continue;
if
(d[j] + m[j][i] > d1[i]) d1[i] = d[j] + m[j][i];
}
}
memcpy(d,d1,sizeof(d1));
t--;
}
Ищем максимальное значение d[i],
среди тех i, для которых fin[i] = 1. Выводим результат.
for(res = i =
0; i < c; i++)
if ((d[i]
> res) && fin[i]) res = d[i];
printf("%d\n",res);
}