10767. Трамваи в Барселоне
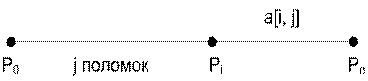
Трамвай должен проехать по
маршруту P0, P1, …, Pn. Расстояние
между остановками Pi-1 и Pi
равно Si. Каждую часть пути Si водитель
должен проезжать с постоянной скоростью vi, которую он
выбирает на остановке Pi-1. Обозначим через Mi
максимально возможную скорость, которую водитель может выбрать на остановке Pi-1
(0 < vi £ Mi). Вероятность поломки трамвая на
промежутке Si равна vi / Mi.
Если поломка имеет место на отрезке Si, то она случается как
раз на середине пути, после чего в течении 10 секунд включается аварийная
система и со скоростью 5 метров в секунду трамвай без поломок едет до остановки
Pi.
Пусть M0 – максимально
допустимая скорость трамвая, с которой он может выехать с начальной станции P0.
Тогда максимальная скорость, с которой трамвай может выехать со станции Pi-1,
равна Mi = M0 – Ci, где Ci
– суммарное количество поломок на промежутках S1, …, Si-1.
Вычисление среднего времени
покажем на примере. Пусть длина пути равна 300 метров, максимально возможная
начальная скорость равна 25 метров в секунду. Если водитель выберет скорость 25
м/с, то трамвай обязательно поломается. И тогда он проедет половину пути за 150
/ 25 = 6 секунд, простоит 10 секунд и доедет с аварийной скоростью 5 м/с до следующей остановки за 150 / 5 = 30 секунд.
Всего при этом потратив 6 + 10 + 30 = 46 секунд. Допустим, что водитель
выбирает скорость 15 метров в секунду. С вероятностью 15 / 25 = 0.6 произойдет
поломка. В случае поломки трамвай проедет 150 метров со
скоростью 15 м/с (потратив на это 10 секунд), потом 10 секунд простоит и со
скоростью 5 м/с доедет до конца (150 / 5 = 30 секунд). С вероятностью
0.4 трамвай не поломается и доедет до следующей остановки за 300 / 15 = 20
секунд. Среднее время равно 0.6 * 50 + 0.4 * 20 = 38 секунд.
В задаче необходимо вычислить
наименьшее среднее время, за которое трамвай может проехать весь путь от
остановки P0 до Pn.
Вход. Каждая строка соответствует
одному тесту и содержит начальную максимально возможную скорость трамвая M0
(5 £ M0
£ 25), значение n (1 £ n £ M0 - 1) а также длины
всех секций S1, …, Sn.
Выход. Для каждого теста вывести
оптимальное среднее время, за которое трамвай проедет весь путь. Результат
выводить с 4 десятичными знаками после запятой.
Пример входа
25 1 900
25 2 900 900
25 2 305.15 980.76
5 1 1000
Пример выхода
102.0000
205.0303
150.0000
210.0000
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Построим формулу среднего времени
для движения трамвая по одному интервалу. Пусть m – максимально
возможная скорость трамвая в начале интервала, s – длина интервала, x
– скорость трамвая на ней. Тогда среднее время движения равно
f(x) = ![]()
![]() +
+ ![]()
![]()

Найдем скорость x, для которой
это время минимально. Раскроим скобки и сгруппируем:
f(x) = ![]() + x
+ x ![]() –
– ![]()
Производная равна
f’(x) = ![]() +
+ ![]() =
= ![]()
Приравняем ее к нулю, и решим
уравнение относительно x: ![]() . Получим оптимальную скорость
. Получим оптимальную скорость
x = ![]()
Пусть a[i, j] – минимальное время, за которое можно доехать
с остановки Pi до конца маршрута при условии, что до этого
было j поломок. Очевидно, что a[n,
i] = 0.
Обозначим через:
T0 = a[i + 1, j] – оптимальное время, за которое можно
доехать с Pi+1 до конца с j поломками,
T1 = a[i + 1, j + 1] – оптимальное время, за которое можно
доехать с Pi+1 до конца с j + 1 поломками.
Тогда среднее время проезда от Pi
до конца равно
f(x) = ![]()
![]() +
+ ![]()
![]()
Приравниваем производную к нулю
(решаем уравнение f’(x) = 0),
вычисляем скорость x, для которой это
время будет минимальным. Она равна
x = 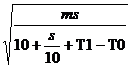
При вычислении a[i, j] следует помнить,
что до Pi было j поломок. Тогда максимально возможная скорость,
которую трамвай может выбрать на Si+1, равна m
= M0 – j. Если вычисленная оптимальная скорость x
будет больше чем M0 – j, то положить x = M0
– j.
Оптимальное среднее время, за
которое трамвай проедет весь путь, равно a[0,
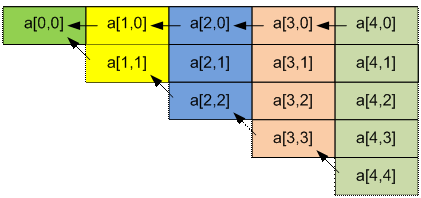
0]. Вычисление значений массива a
идет с конца (сначала вычисляется столбик a[n
– 1, i] (0 £ i £ n – 1), потом a[n
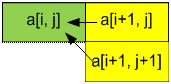
– 2, i] (0 £ i £ n – 2) и так далее до a[0, 0]). Каждое значение a[i,
j] пересчитывается через a[i
+ 1, j] и a[i + 1, j
+ 1].
Пример
Рассмотрим второй тест. Данные
матрицы a вместе с оптимальными
значениями скоростей x приведены в таблице:
|
a[0, 0] = 205.0303 x = 14.8723 |
a[1, 0] = 102.0 x = 15.0 |
a[2, 0] = 0 |
|
|
a[1, 1] = 103.7245 x = 14.6969 |
a[2, 1] = 0 |
|
|
|
a[2, 2] = 0 |
Вычислим a[1, 1].
Оптимальная скорость равна:
x = 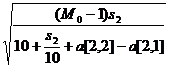 =
=  =
= ![]() =
= ![]() ≈ 14.6969
≈ 14.6969
a[1, 1] = ![]()
![]() +
+ 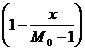
![]() ≈ 103.7245
≈ 103.7245
Вычислим a[1, 0].
Оптимальная скорость равна:
x = 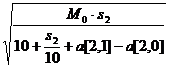 =
= 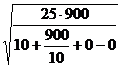 =
= ![]() = 15
= 15
a[1, 0] = ![]()
![]() +
+ 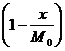
![]() = 102
= 102
Вычислим a[0, 0].
Оптимальная скорость равна:
x = 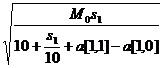 =
= 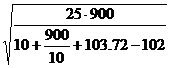 =
= ![]() ≈ 14.8723
≈ 14.8723
a[0, 0] = ![]()
![]() +
+ 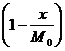
![]() ≈ 205.0303
≈ 205.0303
Реализация алгоритма
Читаем входные данные и обнуляем
последний столбец матрицы a (a[n, i] = 0, 0 £ i £ n).
while(scanf("%lf
%d",&m0,&n) == 2)
{
for(i = 0; i
< n; i++) scanf("%lf",&s[i]);
for(i = 0; i <= n; i++) a[n][i] = 0;
Динамически пересчитываем
значения i - го столбца через i + 1 – ый (0 £ i £ n -1). Данные каждого
столбца вычисляем сверху вниз, двигаясь от a[i, 0] до a[i, i].
for(i = n -
1; i >= 0; i--)
for(j = 0;
j <= i; j++)
{
x = sqrt((m0-j) * s[i] / (10 + s[i]/10 +
a[i+1][j+1] - a[i+1][j]));
if (x
> m0 - j) x = m0 - j;
a[i][j] = (x / (m0-j)) * (s[i]/2/x + 10
+ s[i]/10 + a[i+1][j+1]) +
(1 - x/(m0-j)) * (s[i]/x +
a[i+1][j]);
}
Выводим результат с 4 десятичными знаками после
запятой.
printf("%.4lf\n",a[0][0]);
}