10780. Снова простое число? Нет времени

По заданному натуральному числу n найти максимальную степень числа m (не обязательного простого), которая делит n!.

Вход. Первая строка содержит число k – количество тестов. Далее следует k строк, каждая из которых содержит два числа m (1 < m < 5000) и n (0 < n < 10000), разделенные пробелом. Входные данные содержат не более 500 тестов.

Выход. Для каждого теста вывести его номер и результат в отдельных строках. Результатом будет либо максимальная степень числа m, которая делит n!, либо фраза “Impossible to divide” если n! не делится на m.

Пример входа

2

2 10

2 100

Пример выхода

Case 1:

8

Case 2:

97

РЕШЕНИЕ

математика

Анализ алгоритма

Пусть x – искомая максимальная степень, для которой m^x делит n!.

Если m – простое число, то достаточно найти сколько раз встречается множитель m в разложении n! на простые множители. Тогда:

x =

Суммирование заканчивается, когда выполняется mⁱ > n, так как тогда все последующие слагаемые равны нулю.

Пусть m = – разложение на простые множители. Если множитель p_i входит в разложение n! d_i раз, то значение x не может быть больше чем d_i / a_i. Тогда

x =

Пример

Рассмотрим пример, в котором m = 1440, n = 100. 1440 = 2⁵ * 3² * 5.

Число 2 входит в разложение 100! +++++ = 50 + 25 + 12 + 6 + 3 + 1 = 97 раз, x не больше 97 / 5 = 19;

Число 3 входит в разложение 100! +++ = 33 + 11 + 3 + 1 = 48 раз, x не больше 48 / 2 = 24;

Число 5 входит в разложение 100! + = 20 + 4 = 24 раз, x не больше 24 / 1 = 24;

Таким образом, x не больше (то есть равно) min(19, 24, 24) = 19.

Реализация алгоритма

По условию m < 5000, следовательно простые делители числа m следует перебирать от 2 до = 70. Занесем их в массив

int primes[19] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67};

Функция GetDiv по заданным p и n вычисляет и возвращает сумму .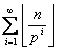

int GetDiv(int p, int n)

{

int res = 0, t = 1;

while (t <= n)

{

t = t * p;

res += (n / t);

}

return res;

}

Для каждого теста читаем входную пару чисел m и n, присваиваем значению x максимально возможное значение (например 100000).

scanf("%d",&tests);

for(TestNo = 1; TestNo <= tests; TestNo++)

{

scanf("%d %d",&m,&n);

x = 100000;

Перебираем простые делители числа m. Для каждого делителя вычисляем степень degree, с которой он входит в число m. Если степень больше нуля, то ищем количество раз d, которое текущий множитель primes[i] входит в разложение n! и пересчитываем значение x.

for(i = 0; i < 19; i++)

{

degree = 0;

while(m % primes[i] == 0)

{

degree++;

m /= primes[i];

}

if (degree > 0)

{

d = GetDiv(primes[i],n);

x = min(x,d/degree);

}

}

Один и только один из простых делителей числа m может быть больше 70 и входить в m с кратностью 1. Если после выполнения выше указанного цикла значение m больше единицы, то m содержит этот делитель, для которого необходимо пересчитать значение x.

if (m > 1)

{

d = GetDiv(m,n);

x = min(x,d);

}

Например, если m = 2² * 3 * 103 = 1236, то таким делителем будет 103.

Если значение x равно нулю, то ни один из простых делителей числа m не входит в разложение n! на простые множители. То есть n! не делится на m и следует вывести фразу о невозможности выполнения деления. Иначе выводим значение x.

if (!x) printf("Case %d:\nImpossible to divide\n",TestNo);

else printf("Case %d:\n%d\n",TestNo,x);

}