10843. Игра Ани

Аня любит играть в следующую игру. Она рисует круг на бумаге. Потом рисует следующий круг и соединяет его отрезком с предыдущим. Затем рисует следующий круг и соединяет его с одним из предыдущих кругов. И так далее пока на бумаге не окажется n кругов. Аня нумерует круги числами от 1 до n в произвольном порядке. Сколько разных рисунков может получить Аня? Рисунки считаются разными, если существуют такие два круга i и j, что в одном рисунке они соединены, а в другом – нет.

Вход. Первая строка содержит количество тестов N. Далее следуют N строк, каждая из которых содержит количество кругов n (0 < n £ 100).

Выход. Для каждого теста вывести его номер и число X, где X – остаток от деления количества разных рисунков на 2000000011.

Пример входа

3
1
2
3

Пример выхода

Case #1: 1
Case #2: 1
Case #3: 3

РЕШЕНИЕ

графы, количество остовных деревьев

Анализ алгоритма

В задаче требуется найти количество разных пронумерованных деревьев с n вершинами. Или то же самое что количество остовных деревьев в полном графе из n вершин (граф называется полным, если его две любые вершины соединены ребром).

Теорема. Существует взаимно однозначное соответствие между остовными деревьями для полного графа из n вершин и кодами Прюфера длины n – 2.

Лемма. Количество кодов Прюфера длины n – 2 равно n^n-2.

Значит количество рисунков, которое может изобразить Аня (число пронумерованных деревьев с n вершинами), равно n^n-2.

Пример

Для n = 4 имеем 16 деревьев. Под каждым деревом приведен его код Прюфера

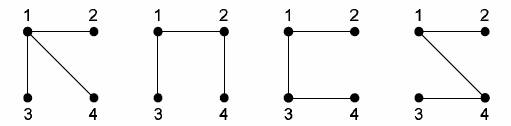
(1, 1) (1, 2) (1, 3) (1, 4)

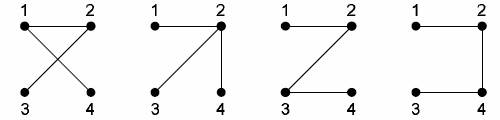
(2, 1) (2, 2) (2, 3) (2, 4)

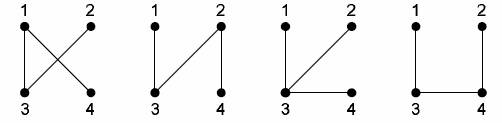
(3, 1) (3, 2) (3, 3) (3, 4)

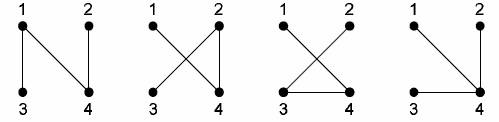
(4, 1) (4, 2) (4, 3) (4, 4)

Реализация алгоритма

Читаем количество тестов tests. Для каждого теста читаем значение n, вычисляем и выводим результат n^n-2 (mod 2000000011) .

long long res;

scanf("%d",&tests);

for(t = 1; t <= tests; t++)

{

scanf("%d",&n);

res = 1;

for(i = 0; i < n - 2; i++)

res = (res * n) % 2000000011;

printf("Case #%d: %lld\n",t,res);

}