11155. Будьте эффективными
Рассмотрим целочисленную
последовательность, состоящую из n элементов:
x0 = a,
xi = ((xi-1
* b) + c) % m + 1, i = 1, 2, …, n – 1.
Заданы числа a,
b, c, m, n. Найти количество “последовательных
подпоследовательностей”, сумма чисел которых делится на m.
Рассмотрим пример, в котором a = 2, b = 1, c = 2, m = 4, n = 4. Тогда
x0 = 2,
xi = (xi-1
+ 2) % 4 + 1, i = 1, 2, 3, 4
Откуда x0
= 2, x1 = 1, x2 = 4, x3 = 3. Последовательными подпоследовательностями будут {2}, {2 1}, {2 1 4}, {2 1 4 3},
{1}, {1 4}, {1 4 3}, {4}, {4 3} и {3}. Из перечисленных 10 подпоследовательностей сумма только
двух делится на 4: {1, 4, 3} и {4}.
Вход. Первая
строка содержит количество тестов t (t < 500). Каждая следующая строка
является отдельным тестом и содержит пять целых чисел: a, b,
c, m, n (0 
a, b, c
1000, 0 < m, n 10000).
Выход. Для каждого теста вывести его
номер и требуемый результат.
Пример входа
3
2 1 2 4 4
923 278 195 8685 793
2 1 3 7 101
Пример выхода
Case 1: 2
Case 2: 34
Case 3: 1323
РЕШЕНИЕ
обработка последовательности
Анализ алгоритма
Находим все элементы
целочисленной последовательности xi и сохраняем их в
массиве x. Находим все частичные суммы построенной последовательности, взятые
по модулю m. Положим
si =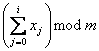 
Сумма xi + xi+1
+ … + xj-1 + xj (0 i j n – 1) делится на m тогда и только тогда, когда s[j]
– s[i – 1] делится на m (здесь s[–1] считаем равным 0).
Пусть для некоторого p имеется такая возрастающая
подпоследовательность индексов i1,
i2, …, ip, что 
= 
= … = 
. Это значит, что 
– 
= 0 для любых q, t
(1 t < q p). Любая пара 
взаимно однозначно
определяет “последовательную
подпоследовательность”, причем если разница – равна 0, то сумма элементов соответствующей
подпоследовательности делится на m. Таких
пар будет в точности p * (p – 1) / 2.
Таким
образом, количество последовательных подпоследовательностей в xi, сумма элементов которых
делится на m, равно числу пар (si,
sj), где si = sj и –1 i
< j < n (s-1 всегда равно 0). Заполняем массив mod, в котором mod[k] содержит количество элементов s[i], равных k (0 k < m). Остается
просуммировать количество указанных пар (si, sj). Оно
равно
Пример
Рассмотрим третий пример.
Рекурентность имеет вид:
x0 = 2,
xi = (xi-1
+ 3) % 7 + 1, i = 1, …, 100
Последовательность x будет периодической: {2, 6, 3, 7, 4, 1, 5, 2,
…, 2, 6, 3}. Период
последовательности состоит из 7 чисел. Например x0 = x7 = x14 = … x98 = 2. То есть наша последовательность состоит из 98 /
7 = 14 полных блоков из 7 чисел плюс пятнадцатый неполный блок, состоящий из трех
чисел {x98 = 2, x99 = 6, x100 = 3}.
Массив частичных сумм s также
будет иметь периодический вид: {2, 1, 4, 4, 1, 2, 0, 2, …, 2, 1, 4}. И его также можно разбить на 14 полных блоков по 7 чисел {2, 1, 4, 4, 1, 2, 0} и остаток {2, 1, 4}. Нулей
в массиве s в точности 14, двоек, единиц и четверок – по 14 * 2 + 1 = 29.
Если в паре (si,
sj) первый индекс i = -1, то рассматриваемая
подпоследовательность начинается с x0. Следовательно
при построении массива mod необходимо учесть еще и значение s[–1] = 0. То есть массив mod выглядит так: {15, 29, 29, 0, 29, 0, 0}.
Согласно приведенной формуле количество “последовательных
подпоследовательностей” равно 
= 
= 
= 1323.
Реализация алгоритма
Последовательность xi содержит не более MAXN = 10000
элементов, s[i] содержит сумму первых
i элементов последовательности xi,
взятую по модулю m, mod[i] содержит количество элементов s[j], равных i.
#define MAXN 10000
int x[MAXN], s[MAXN],
mod[MAXN];
Читаем количество тестов tests. Для каждого теста вводим входные
данные.
scanf("%d",&tests);
for(t = 1; t <= tests; t++)
{
scanf("%d %d %d %d %d",&a,&b,&c,&m,&n);
Вычисляем элементы
последовательности x[i] и сумм s[i].
x[0] = a; s[0] = a % m;
for(i = 1; i < n; i++)
x[i] = (x[i-1] *
b + c) % m + 1,
s[i] = (s[i-1] + x[i]) % m;
Вычисляем элементы mod[i], равные количеству элементов s[j], равных i.
memset(mod,0,sizeof(mod));
for(i = 0; i < n; i++) mod[s[i]]++;
Поскольку s[–1] = 0, то следует увеличить mod[0]
на 1. Находим результат по выше приведенной формуле и выводим его.
mod[0]++; res = 0;
for(i = 0; i < m; i++)
res += (mod[i] * (mod[i] - 1)) / 2;
printf("Case %d: %d\n",t,res);
}