11186. Вписанные треугольники

На границе окружности с центром в начале координат и радиусом R заданы N точек. Так как все точки расположены на одной окружности, никакие три из них не колинеарны. Поэтому любые три точки образуют невырожденный треугольник. Вычислить сумму площадей всех треугольников.

Вход. Содержит не более 16 тестов. Каждый тест начинается строкой, содержащей два целых числа: количество точек N (0 £ N £ 500) и радиус окружности R (0 < R £ 100). Далее следуют N строк, каждая из которых описывает положение точки P_i на окружности действительным числом theta (0.00 < theta £ 360.00). Значение theta является углом наклона в градусах отрезка P_iO к оси абсцисс (O – начало координат). То есть декартовыми координатами точки P_i будут (x, y) = (R * cos(theta), R * sin(theta)).

Последний тест содержит N = R = 0 и не обрабатывается.

Выход. Для каждого теста вывести сумму площадей всех треугольников, округленную до ближайшего целого.

Пример входа

5 10

10.00

100.00

300.00

310.00

320.00

3 20

10.00

100.00

300.00

0 0

Пример выхода

286

320

РЕШЕНИЕ

геометрия + перебор

Анализ алгоритма

Рассмотрим треугольник ABC. Вычислим его площадь как площадь круга минус площадь трех черных сегментов, как показано на рисунке.

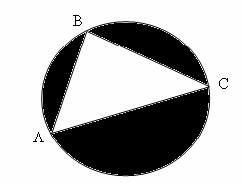
Таким образом, искомая площадь равна минус суммарная площадь сегментов, которую как далее будет показано, можно вычислить за время O(n²).

Напомним, что площадь сектора радиуса R, стягиваемого углом a, равна . Площадь соответствующего сегмента равна площади сектора минус площадь равнобедренного треугольника с боковой стороной R и углом при вершине a. Таким образом, площадь сегмента равна

S_{сегмента} = =

Изначально положим искомую площадь всех треугольников равной res = = . После чего из res будем последовательно вычитать площади сегментов.

Рассмотрим отрезок, соединяющий точки P_i и P_j (i < j). В переменной s вычислим площадь сегмента, который мы проходим при движении по окружности от точки P_i к P_j против часовой стрелки (по направлению возрастания углов).

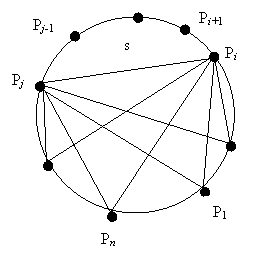
Сегмент площади s вычитается из общей площади res столько раз, сколько точек находится между P_i и P_j со стороны сегмента площади . Сегмент площади s вычитается при подсчете площадей треугольников P_iP_jP_k, где k пробегает по точкам, расположенным от P_j до P_i при движении против часовой стрелки (k принимает значения j + 1, j + 2, …, i – 2, i – 1). Таких точек будет pnts1 = n – (j – i + 1). Вычитаем из res pnts1 раз площадь s.

Соответственно точек со стороны сегмента площади s будет pnts2 = n – pnts1 – 2. Именно столько раз необходимо вычитать площадь сегмента из res.

Реализация алгоритма

Считаем градусную меру точек, переведем ее в радианную и занесем в ячейки массива d (d[i] содержит радианную меру i - ой точки).

double alfa, sq, d[MAX];

Пока не достигнем конца файла, читаем входные данные.

while(scanf("%d %d",&n,&r), n + r)

{

Заносим радианную меру точек в массив d, сортируем массив d по возрастанию.

for(i = 0; i < n; i++) scanf("%lf",&d[i]), d[i] = d[i] * PI / 180;

sort(d,d + n);

В переменную res изначально заносим площадь, равную площади кругов радиуса R, то есть значение = . Переменной r2 присвоим значение , а sq площадь одного круга, то есть .

res = n * (n - 1) * (n - 2) / 6 * PI * r * r;

r2 = r * r / 2.0; sq = PI * r * r;

При помощи индексов i и j совершаем перебор пар точек.

for(i = 0; i < n; i++)

for(j = i + 1; j < n; j++)

{

Вычисляем угол alfa между точками i и j, который равен d[j] – d[i]. Если alfa меньше , то при движении от i к j мы проходим по меньшему сегменту и его площадь равна . Иначе при движении от i к j мы проходим по большему сегменту и в таком случае его площадь равна , где положено .

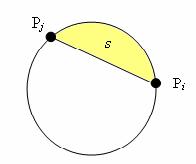
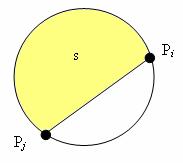
В обоих случаях переменной s присваивается площадь сегмента, который мы проходим при движении от P_i к P_j против часовой стрелки.

alfa = d[j] - d[i];

if (alfa < PI)

s = r2 * (alfa - sin(alfa));

else

{

alfa = 2 * PI - alfa,

s = sq - r2 * (alfa - sin(alfa));

}

Количество точек points, лежащих на сегменте, площадь которого , равно n – (j – i + 1). Таким образом из значения res необходимо вычесть points раз площадь сегмента s.

points = n - (j - i + 1);

res -= s * points;

Количество точек, лежащих на сегменте площади s, равно points = n – points – 2. Площадь противоположного сегмента равна sq – s. Остается вычесть ее из res points раз.

points = n - points - 2;

res -= (sq - s) * points;

}

Выводим на печать искомую площадь res.

printf("%.0lf\n",res);

}