11401. Подсчет треугольников
Имеется n стержней с длинами 1, 2, …, n. Вы можете выбрать любые три из них и
построить треугольник. Сколько различных треугольников можно построить? Два
треугольника считаются различными, если у них есть как минимум одна пара сторон
с разными длинами.
Вход. Каждая строка содержит значение n (3 ≤ n ≤ 1000000).
Последний тест содержит n < 3 и не
обрабатывается.
Выход. Для каждого
входного значения n в отдельной
строке вывести количество различных треугольников, которое можно построить.
|
Пример
входа |
Пример
выхода |
|
5 8 0 |
3 22 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Обозначим через
T(n) количество различных
треугольников, которое можно построить из n
стержней. Вычислим некоторые значения функции:
·
T(3) = 0, из стержней с длинами 1, 2 и 3 составить
треугольник нельзя;
·
T(4) = 1, треугольник (2, 3, 4);
·
T(5) = 3, треугольники (2, 3, 4), (2, 4, 5), (3, 4, 5);
·
T(6) = 7, треугольники (2, 3, 4), (2, 4, 5), (3, 4, 5), (4,
5, 6), (3, 5, 6), (2, 5, 6), (3, 4, 6);
Очевидно, что T(n) включает в себя все тройки T(n – 1). Будем рассматривать множество T(n) как множество T(n – 1) плюс все тройки, которые содержат стержень длины n (назовем это множество S(n)). Например
T(6) = T(5) È { (4, 5, 6),
(3, 5, 6), (2, 5, 6), (3, 4, 6) }
Рассмотрим, какие
числа кроме n содержит множество S(n). Например, если тройка из S(n) содержит n – 1, то вместе с n – 1
она может содержать числа n – 2, n – 3, …, 2 (сумма n – 1 и любого из этих чисел больше n, в результате чего тройка может образовывать треугольник). Если
тройка из S(n) содержит n – 2, то вместе с n – 2 она может содержать числа n
– 3, n – 4, …, 3. И так далее.
Рассмотрим множество
S(6):
·
Вместе с числом 5 могут быть числа 2, 3, 4 – образуя
тройки (2, 5, 6), (3, 5, 6), (4, 5, 6);
·
Вместе с числом 4 может быть только число 3 – образуется
тройка (3, 4, 6);
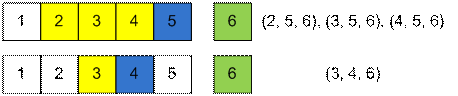
Поскольку S(6)
содержит 1 + 3 = 4 элемента, то T(6) = T(5) + |S(6)| = 3 + 4 = 7.
Рассмотрим
множество S(7):
·
Вместе с числом 6 могут быть числа 2, 3, 4, 5 – образуя
тройки (2, 6, 7), (3, 6, 7), (4, 6, 7),
(5, 6, 7);
·
Вместе с числом 5 могут быть числа 3, 4 – образуя тройки (3, 5, 7), (4, 5, 7);

Поскольку S(7)
содержит 2 + 4 = 6 элементов, то T(7) = T(6) + |S(7)| = 7 + 6 = 13.
Проводя подобные
исследования, можно заметить что
·
при четном n
значение S(n) содержит 1 + 3 + 5 + …
+ (n – 3) = 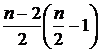 элементов;
элементов;
·
при нечетном n
значение S(n) содержит 2 + 4 + 6 + …
+ (n – 3) = ![]() элементов;
элементов;
Таким образом
получим рекуррентность:
·
при четном n
имеем: T(n) = T(n – 1) + 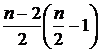 ;
;
·
при нечетном n
имеем: T(n) = T(n – 1) + ![]() ;
;
Значение T(n) можно также выразить в явном виде:
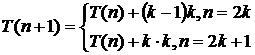 или
или 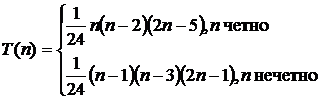
Последовательность
T(n) имеет производящую функцию
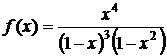 = x4 + 3x5
+ 7x6 + 13x7 + …
= x4 + 3x5
+ 7x6 + 13x7 + …
Пример

Реализация алгоритма
Объявим массив
для запоминания.
#define MAX 1000001
long long T[MAX];
Основная часть программы. Заполним массив T.
memset(T,0,sizeof(T));
for(i = 4; i < MAX; i++)
if (i % 2 == 0) T[i] = T[i-1] + (i - 2)
/ 2 * (i / 2 - 1);
else T[i] = T[i-1] + (i - 1) * (i - 3) /
4;
Обрабатываем последовательно запросы.
while(scanf("%lld",&n),
n >= 3)
printf("%lld\n",T[n]);
Реализация алгоритма – формула
Реализация
функции T(n).
long long
T(long long n)
{
if (n % 2) return (n - 1) * (n - 3) * (2 * n - 1) / 24;
return n * (n
- 2) * (2 * n - 5) / 24;
}
Основной цикл программы.
while(scanf("%lld",&n),
n >= 3)
printf("%lld\n",T(n));