190. Окружность через три точки
На плоскости заданы три точки, не
лежащие на одной прямой. Необходимо найти уравнение окружности, проходящей
через эти три точки. Уравнение окружности имеет один из следующих видов: (x – a)2
+ (y – b)2 = r2
или x2 + y2 + cx + dy + e = 0.
Вход. Каждая
строка содержит шесть действительных чисел Ax, Ay, Bx,
By, Cx, Cy – координаты трех точек A(Ax,
Ay), B(Bx, By), C(Cx, Cy).
Выход. Для каждой тройки точек вывести
уравнение окружности, проходящей через них в двух форматах, как показано ниже. После
каждой пары строк, содержащих уравнения окружности, выводить пустую строку.
Действительные числа выводить с тремя знаками после запятой.
Пример входа
7.0 -5.0 -1.0 1.0 0.0 -6.0
1.0 7.0 8.0 6.0 7.0 -2.0
Пример выхода
(x - 3.000)^2 + (y + 2.000)^2 = 5.000^2
x^2 + y^2 - 6.000x + 4.000y - 12.000 = 0
(x - 3.921)^2 + (y - 2.447)^2 = 5.409^2
x^2 + y^2 - 7.842x - 4.895y - 7.895 = 0
РЕШЕНИЕ
геометрия
Анализ алгоритма
Построим серединные
перпендикуляры к отрезкам AB и AC. Точка их пересечения и будет центром искомой
окружности О. Радиус окружности равен расстоянию OA.
Реализация алгоритма
Функция kramer решает систему линейных уравнений 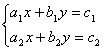 методом Крамера
методом Крамера
d = 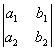 , dx =
, dx = 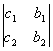 , dy =
, dy = 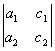 , x =
, x = ![]() , y =
, y = ![]() , d ¹ 0
, d ¹ 0
и возвращает:
·
0, если система имеет единственное решение;
·
1, если система не имеет решений (прямые параллельны и не
совпадают);
·
2, если система имеет бесконечное количество решений
(прямые совпадают);
int kramer(double
a1,double b1, double
c1,
double
a2,double b2, double
c2, double *x, double
*y)
{
double d = a1
* b2 - a2 * b1;
double dx =
c1 * b2 - c2 * b1;
double dy =
a1 * c2 - a2 * c1;
if (!d) return (dx == 0.0) + 1;
*x = dx/d; *y = dy/d;
return 0;
}
Функция midperpend
по заданным координатам концов отрезка A(x1,
y1) и B(x2, y2) строит серединный перпендикуляр ax + by + c = 0. Поскольку вектора AB(x2 – x1, y2
– y1) и (a, b)
коллинеарны, то
a = x2 – x1,
b = y2 – y1
Серединный
перпендикуляр проходит через точку ![]() – середину отрезка АВ,
значит ax + by + c = (x2 – x1)
– середину отрезка АВ,
значит ax + by + c = (x2 – x1) ![]() + (y2 – y1)
+ (y2 – y1) ![]() + c = 0, откуда c =
+ c = 0, откуда c = ![]() .
.
void midperpend(double
x1, double y1, double
x2, double y2,
double
*a, double *b, double
*c)
{
*a = x2 - x1;
*b = y2 - y1;
*c = (x1*x1 - x2*x2 + y1*y1 - y2*y2) / 2;
}
Функция
circle по трем точкам A(x1,
y1), В(x2, y2) и С(x3,
y3) находит центр
окружности (xc, yc) и радиус r, который
через них проходит. Для этого строятся серединные перпендикуляры к отрезкам AB
и AC, после чего находится точка их пересечения О – центр искомой
окружности. Радиус r вычисляется как расстояние между точками O и A.
void circle(double
x1, double y1, double
x2, double y2, double
x3, double y3,
double
*xc, double *yc, double
*r)
{
double
a1,b1,c1,a2,b2,c2;
midperpend(x1,y1,x2,y2,&a1,&b1,&c1);
midperpend(x1,y1,x3,y3,&a2,&b2,&c2);
kramer(a1,b1,-c1,a2,b2,-c2,xc,yc);
*r = sqrt((x1 - *xc)*(x1 - *xc) + (y1 -
*yc)*(y1 - *yc));
}
Для каждого теста находим
окружность, проходящую через три точки, и выводим данные о ней в соответствии с
требуемым форматом.
while(scanf("%lf
%lf %lf %lf %lf %lf",&x_1,&y_1,&x_2,&y_2,&x_3,&y_3)
== 6)
{
circle(x_1,y_1,x_2,y_2,x_3,y_3,&xc,&yc,&r);
printf("(x");
if (xc >=
0.0) printf(" - "); else printf(" +
");
printf("%.3lf)^2
+ (y",fabs(xc));
if (yc >=
0.0) printf(" - "); else printf(" +
");
printf("%.3lf)^2
= %.3lf^2\n",fabs(yc),r);
printf("x^2 +
y^2");
if (xc >=
0.0) printf(" - "); else printf(" +
");
printf("%.3lfx",2*fabs(xc));
if (yc >=
0.0) printf(" - "); else printf(" +
");
printf("%.3lfy",2*fabs(yc));
r1 = xc*xc + yc*yc - r*r;
if (r1 >=
0.0) printf(" + "); else printf(" -
");
printf("%.3lf
= 0\n\n",fabs(r1));
}