200. Редкий порядок
В некотором
алфавитном порядке записаны слова. Найти этот алфавитный порядок.
Вход. Каждая входная строка содержит слово, состоящее не более
чем из 20 заглавных букв латинского алфавита. Строка, содержащая единственный
символ ‘#’, является маркером конца входных данных и не обрабатывается.
Выход. Единственная
строка из заглавных букв, указывающая алфавитный порядок, в котором заданы
входные слова.
|
Пример
входа |
Пример
выхода |
XWYZXZXYZXWYWWX
# |
XZYW |
РЕШЕНИЕ
графы,
топологическая сортировка
Анализ алгоритма
Из каждой пары
соседних слов выясняем соотношение между некоторыми двумя буквами алфавита.
Полезной информации получить нельзя, если одно из слов является продолжением
другого. Строим ациклический граф, в котором вершинам соответствуют буквы
алфавита, а ребра – отношению «меньше». Запускаем алгоритм топологической
сортировки, в результате выполнения которого получим одну из возможных
расстановок букв в алфавите.
Пример
Со слов XWY и ZX
получим соотношение: X < Z;
Со слов ZX и ZXY
не возможно получить полезной информации;
Со слов ZXY и
ZXW получим соотношение: Y < W;
Со слов ZXW и
YWWX получим соотношение: Z < Y;
Получили
ациклический граф:
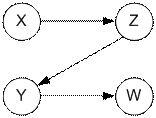
Результатом
топологической сортировки будет последовательность XZYW.
Реализация алгоритма
Строки s1 и s2
будут содержать последовательные входные слова. Граф может содержать максимум
26 вершин (пронумерованных
от 0 до 25), которые
соответствуют буквам латинского алфавита, его матрицу смежности храним в
массиве m. Массив TopSort будет содержать последовательность топологически отсортированных
вершин.
#define MAX 26
char s1[MAX], s2[MAX];
int m[MAX][MAX], used[MAX],
TopSort[MAX];
Поиск в глубину
с топологической сортировкой совершается функцией dfs:
void dfs(int
v)
{
used[v] = 1;
for(int to = 0; to < 26; to++)
if
(!used[to] && m[v][to]) dfs(to);
TopSort[ptr++] = v;
}
Основная часть программы. Читаем словарь, заносим каждую
соседнюю пару слов в массивы s1 и s2. Сравнивая их, находим такую минимальную позицию
i (0 £ i < min(|s1|,|s2|)), для которой буквы s1[i]
и s2[i] не совпадают. Если такой позиции i нет, то одно из слов
является продолжением другого и полезной информации из текущей пары слов
получить нельзя. Иначе буква s1[i] считается меньше s2[i], в граф
заносим ребро s1[i] ® s2[i]. Изначально занесем
в массив used значения 1, считая, что все вершины графа уже отмечены. При
добавлении в граф ребра i ® j будем
отмечать вершины i и j не пройденными.
memset(m,0,sizeof(m));
memset(used,1,sizeof(used));
gets(s1);
while(gets(s2), s2[0] != '#')
{
int temp =
min(strlen(s1),strlen(s2));
for(i = 0; i
< temp; i++)
if (s1[i]
!= s2[i])
{
m[s1[i] - 'A'][s2[i]
- 'A'] = 1;
used[s1[i] - 'A']
= used[s2[i] - 'A'] = 0;
break;
}
strcpy(s1,s2);
}
Граф может быть
не связным, совершаем поиск в глубину и заносим последовательность
топологически отсортированных вершин в массив TopSort.
for(i = 0; i < 26; i++)
if (!used[i]) dfs(i);
Выводим массив
топологически отсортированных вершин – один из возможных алфавитов, в котором
заданы входные слова.
while(--ptr >= 0) printf("%c",TopSort[ptr] + 'A');
printf("\n");