216. Выстраивание в линию
Имеется набор из не более чем 8
компьютеров. Местоположение каждого компьютера описывается декартовыми
координатами. Все компьютеры необходимо соединить при помощи кабеля в сеть,
имеющую вид ломанной. Найдите такое соединение компьютеров в сеть, при котором
длина использованного кабеля будет наименьшей.
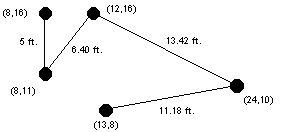
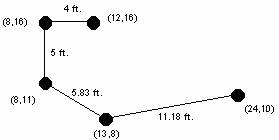
Например, ниже представлены два
возможных метода соединения коппьютеров. Второе соединение является
оптимальным, так как в нем общая длина кабеля среди всех возможных соединений
будет наименьшей (90.01 фута).
Кабель между компьютерами тянется
по полу. Поэтому длина кабеля, соединяющего два компьютера, равна расстоянию
между ними плюс 16 футов дополнительно, которые соединяют компьютерные столы с
полом.
Вход. Состоит из нескольких тестов. Первая строка теста
содержит количество компьютеров n (n £ 8). Следующие n строк задают координаты
компьютеров. Координатами являются целые числа от 0 до 150. Никакие два
компьютера не имеют одинаковых координат. Последний тест содержит n
= 0 и не обрабатывается.
Выход. Для каждого теста в отдельной
строке вывести его номер. Далее для каждого кабеля, соединяющего соседние
компьютеры в сети, вывести его характеристики, как показано в примере. Последняя
строка должна содержать общую длину кабеля. Длины выводить с двумя точками
после запятой. Тесты разделять строкой из символов ‘*’.
Пример входа
6
5 19
55 28
38 101
28 62
111 84
43 116
5
11 27
84 99
142 81
88 30
95 38
3
132 73
49 86
72 111
0
Пример выхода
**********************************************************
Network #1
Cable requirement to connect (5,19) to (55,28) is 66.80 feet.
Cable requirement to connect (55,28) to (28,62) is 59.42
feet.
Cable requirement to connect (28,62) to (38,101) is 56.26
feet.
Cable requirement to connect (38,101) to (43,116) is 31.81
feet.
Cable requirement to connect (43,116) to (111,84) is 91.15
feet.
Number of feet of cable required is 305.45.
**********************************************************
Network #2
Cable requirement to connect (11,27) to (88,30) is 93.06
feet.
Cable requirement to connect (88,30) to (95,38) is 26.63
feet.
Cable requirement to connect (95,38) to (84,99) is 77.98
feet.
Cable requirement to connect (84,99) to (142,81) is 76.73
feet.
Number of feet of cable required is 274.40.
**********************************************************
Network #3
Cable requirement to connect (132,73) to (72,111) is 87.02
feet.
Cable requirement to connect (72,111) to (49,86) is 49.97
feet.
Number of feet of cable required is 136.99.
РЕШЕНИЕ
комбинаторика, генерация перестановок
Анализ алгоритма
Составим матрицу d расстояний
между компьютерами. Положим d[i][j] равным длине кабеля, соединяющего i - ый и j - ый компьютеры.
Генерируем все возможные перестановки x1, x2, …, xn
чисел от 1 до n. Каждая перестановка соответствует соединению
компьютеров в линию (компьютер xi соединен с компьютером xi+1,
i = 1, …, n – 1). Для каждой перестановки вычисляем длину
использованного кабеля. Среди всех возможных перестановок (расположений в линию)
выбираем ту, для которой длина кабеля наименьшая.
Реализация алгоритма
Координаты компьютеров храним в
массивах x и y. В массиве perm будем генерировать все возможные перестановки
чисел от 0 до n – 1. В массиве p
будет запоминаться искомая (оптимальная) перестановка. В переменной asterix храним строку из 58 символов
‘*’, которой следует разделять тесты. В массиве d храним расстояния между
компьютерами.
string
asterix(58,'*');
int i, j, n, c = 1;
int x[8], y[8];
vector<int> p, perm;
double len, MinLen, d[8][8];
Читаем количество компьютеров n для текущего теста. Устанавливаем
текущее значение длины использованного кабеля MinLen равным наибольшему числу.
while(scanf("%d",&n),n)
{
perm.clear(); MinLen = 2E9;
Читаем координаты n компьютеров, инициализируем массив
perm для генерации в нем всех перестановок в лексикографическом порядке.
for(i = 0; i
< n; i++)
scanf("%d %d",&x[i],&y[i]),perm.push_back(i);
Вычисляем расстояния между всеми
парами компьютеров, заносим их в массив d. К каждому расстоянию добавляем 16
футов, как указано в условии задачи.
for(i = 0; i
< n; i++)
for(j = 0;
j < n; j++)
d[j][i] = d[i][j] =
sqrt(1.0*(y[j]-y[i])*(y[j]-y[i]) +
(x[j]-x[i])*(x[j]-x[i])) + 16;
Выводим строку из 58 звездочек и
номер теста (сети).
printf("%s\n",asterix.c_str());
printf("Network #%d\n",c++);
Генерируем все перестановки
компьютеров и для каждой перестановки вычисляем длину использованного кабеля.
Если текущая перестановка лучше предыдущей, то найденную общую длину кабеля len запоминаем в переменной MinLen, а перестановку – в массиве p.
do{
for(len = i
= 0; i < n - 1; i++) len += d[perm[i]][perm[i+1]];
if (len
< MinLen) MinLen = len,p = perm;
} while(next_permutation(perm.begin(),perm.end()));
Выводим длины кабелей, используя оптимальную
перестановку в массиве p.
for(i = 0; i
< n - 1; i++)
printf("Cable
requirement to connect (%d,%d) to (%d,%d) is %.2lf
feet.\n",x[p[i]],y[p[i]],x[p[i+1]],y[p[i+1]],d[p[i]][p[i+1]]);
printf("Number
of feet of cable required is %.2lf.\n",MinLen);
}