374. Большой модуль

По заданным b, p, m вычислить значение выражения b^p mod m.

Вход. Содержит несколько тестов. Числа b, p, m находятся в отдельных строках. Известно, что 0 £ b, p £ 2147483647, 1 £ m £ 46340.

Выход. Для каждого теста вывести в отдельной строке значение b^p mod m.

Пример входа	Пример выхода
3 18132 17 17 1765 3 2374859 3029382 36123	13 2 13195

РЕШЕНИЕ

рекуррентное соотношение

Анализ алгоритма

Из ограничений на входные данные следует, что в процессе вычисления достаточно использовать тип данных int. Возведение в степень b^p будем производить с логарифмической временной сложностью O(log p) используя алгоритм, базирующийся на двоичном разложении показателя степени p:

b^p =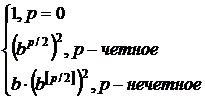

Пример

Для вычисления значения из первого теста 3¹⁸¹³² (mod 17) следует представить показатель степени в двоичной системе исчисления: 18132₁₀ = 100011011010100₂. Далее 3¹⁸¹³² (mod 17) = 3¹⁶³⁸⁴ * 3¹⁰²⁴ * 3⁵¹² * 3¹²⁸ * 3⁶⁴ * 3¹⁶ * 3⁴ (mod 17) = 13.

Для второго теста 17¹⁷⁶⁵ (mod 3) = (17 mod 3) ¹⁷⁶⁵ (mod 3) = 2 ¹⁷⁶⁵ (mod 3) = 2.

Реализация алгоритма

Функция pow вычисляет выражение b^p mod m с оценкой сложности O(log p).

int pow(int b, int p, int m)

{

int res = 1;

while(p > 0)

{

if (p & 1) res = (res * b) % m;

p >>= 1;

b = (b * b) % m;

}

return res;

}

Прочитав входные значения b, p и m, следует воспользоваться формулой

b^p mod m = (b mod m)^p mod m

При передаче параметров функции pow основание степени b должно быть не больше чем модуль m. Если этого не сделать, получим Time Limit. Отдельно следует обработать случай, когда p = 0: b⁰ mod m = 1.

while (scanf("%d %d %d", &b, &p, &m) == 3)

{

b = b % m;

if (!p) res = 1; else res = pow(b,p,m);

printf("%d\n",res);

}