557. Булочки

У Рональда Макдональда есть n булочек (n четно), среди которых одинаковое количество гамбургеров и чизбургеров. Он раздает их всем детям следующим образом. Рональд берет и бросает монетку. Если выпал орел, то ребенок получает гамбургер, если решка – то чисбургер. Бен и Билл получают свои булочки последними (когда n – 2 булочек уже роздано). Когда Рональд дошел до их очереди, оказалось что бросать монетку нет смысла, так как у него остались булочки одинакового типа. Найти вероятность того, что Бен и Билл получат одинаковый тип булочек (или два гамбургера, или два чизбургера)

Вход. Первая строка содержит количество тестов. Каждая следующая строка содержит четное натуральное число n (1 £ n £ 100000).

Выход. Для каждого теста вывести вероятность того, что Бен и Билл получат одинаковые булочки.

Пример входа

3

6

10

256

Пример выхода

0.6250

0.7266

0.9500

РЕШЕНИЕ

вероятность

Анализ алгоритма

Вычислим вероятность противоположного события X – того, что Бен и Билл получат разные булочки. Для этого среди первых n – 2 разданых детям булочек ровно половина должна быть гамбургерами, половина – чизбургерами.

Рассмотрим схему испытаний Бернулли, где вероятность успеха (например, появления гамбургера) равна p = 1/2, а неуспеха q = 1 – p = 1/2. Вероятность того, что среди n – 2 раздач будет ровно (n – 2) / 2 гамбургеров, равна

P(X) = =

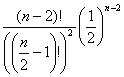
Остается для каждого входного n вычислить значение P(X) и вывести 1 – P(X).

Хотя P(X) лежит в промежутке от 0 до 1 включительно, возможны проблемы с его непосредственным вычислением. Прологарифмируем равенство:

ln P(X) = ln(n – 2)! – –

После вычисления правой части равенства, возведем е в него, получив P(X). Логарифм факториала вычислим как сумму логарифмов:

ln n! = ln 1 + ln 2 + ln 3 + … + ln n

Пример

Для n = 6 вероятность того, что Бен и Билл получат разные булочки, равна

= =

Вероятность того, что Бен и Билл получат одинаковые булочки, равна 1 – = = 0,625.

Реализация алгоритма

Поскольку на вход подается несколько тестов, то для прохождения задачи по времени предвычислим все результаты. В массиве lf будем хранить натуральные логарифмы факториалов натуральных чисел (lf[i] = ln i!), в ячейках массива ans – вероятность того, что среди n – 2 раздач будет ровно (n – 2) / 2 гамбургеров и (n – 2) / 2 чизбургеров.

#define MAX 100001

int i, n, tests;

double lf[MAX], ans[MAX], res;

int main(void)

{

res = lf[1] = 0.0;

Заполним массив lf, положив lf[i] = ln i! = ln 1 + ln 2 + ... + ln n.

for(res = 0, i = 2; i < MAX; i++)

{

res += log((double)i);

lf[i] = res;

}

Заполним массив ans, положив ans [i] = 1 – P(X) = ln(i – 2)! – – .

for(i = 2; i < MAX; i += 2)

{

res = lf[i/2-1];

res = lf[i-2] - (i - 2) * log(2.0) - res - res;

ans[i] = exp(res);

}

Читаем входные данные. Для каждого входного n выводим 1 – ans[n].

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

printf("%.4lf\n",1 - ans[n]);

}

return 0;

}