674. Размен монет
В наличии имеются 5
номиналов монет: 50, 25, 10, 5 и 1 центовые. Сколькими способами можно выдать
наперед заданную сумму s?
Вход. Каждая строка содержит сумму s (s £ 7489).
Выход. Для
каждой суммы вывести количество способов, которыми можно ее выдать.
Пример входа
11 Пример выхода
4 РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Обозначим
через f(k, n) количество способов составить сумму n из
первых k номиналов монет. Оно равно количеству способов составить сумму n
первыми (k – 1) номиналами (то есть без использования k-го
номинала) плюс количество способов составить сумму (n – ak)
при помощи k номиналов. Имеем соотношение:
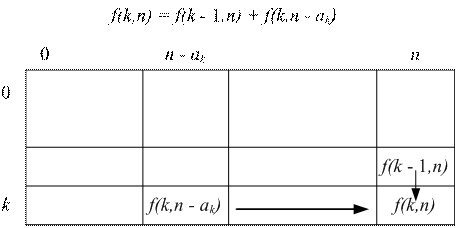
Изначально положим f(0, 0) = 1, f(0, n) = 0, n > 0.
Пример
Сумму s = 11 можно
выдать 4 способами:
1) 10 + 1
2) 5 + 5 + 1
3) 5 + 1 + 1 + 1 + 1 + 1 + 1
4) 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
+ 1
|
|
k \ n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
начало |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
c = 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
c = 5 |
2 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
|
c = 10 |
3 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
4 |
4 |
Номиналы в 25 и 50 центов
не повлияют на результат для суммы в 11 центов.
Реализация алгоритма
Ячейка mas[i] будет содержать количество способов, которыми можно
выдать сумму i. Размер массива
установим MAX = 7490. Номиналы монет занесем в массив coins.
const int
MAX = 7490;
int mas[MAX];
int coins[5] = {1,5,10,25,50};
Динамически пересчитываем массив mas для каждого номинала (всего 5 циклов) согласно выше
приведенному соотношению.
memset(mas,0,sizeof(mas));
mas[0] = 1;
for(i = 0; i < 5; i++)
{
for(j = coins[i]; j < MAX; j++)
mas[j] += mas[j -
coins[i]];
}
Читаем входные суммы и печатаем результат.
while(scanf("%d",&n)
== 1)
printf("%d\n",mas[n]);