2. Цифры
Вычислить
количество цифр целого неотрицательного числа n.
Вход. Одно
неотрицательное целое число n (0
≤ n ≤ 2*109).
Выход. Количество
цифр в числе n.
|
Пример входа |
Пример выхода |
|
13243 |
5 |
РЕШЕНИЕ
элементарная задача
Анализ алгоритма
Количество цифр в
числе можно найти:
·
при помощи одного цикла.
·
при помощи рекурсии,
воспользовавшись рекуррентным соотношением:
digits(n) = 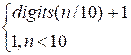
Реализация алгоритма
Читаем входное значение n. Если n = 0, то
ответом будет 1. Иначе инициализируем res нулем и подсчитываем
количество цифр в числе n.
scanf("%d",&n);
res = (n == 0);
while(n > 0)
{
n /= 10;
res++;
}
printf("%d\n",res);
Реализация
алгоритма – рекурсия
#include <stdio.h>
int n, res;
int digits(int
n)
{
if (n < 10) return
1;
return 1 + digits(n / 10);
}
int main(void)
{
scanf("%d",&n);
res = digits(n);
printf("%d\n",res);
return 0;
}
Java реализация
import java.util.*;
public class Main
{
static int digits(int n)
{
if (n < 10) return 1;
return 1 + digits(n / 10);
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int res = digits(n);
System.out.println(res);
con.close();
}
}
Python
реализация
Преобразуем
входное число n в строку, после чего
возьмем ее длину.
n = int(input())
print(len(str(n)))
Если перед числом находятся пробелы,
то следующая реализация не пройдет:
s = str(input())
print(len(s))
Реализация при помощи цикла while:
x = int(input())
cnt = 0
if x == 0:
print ("1")
else:
while x > 0:
cnt += 1
x = x // 10
print (cnt)
Python
реализация – рекурсия
def f(n):
if n < 10:
return 1
return f(n / 10) + 1
n = int(input())
print (f(n))