2. Цифри

Підрахувати кількість цифр цілого невід'ємного числа n.

Вхід. Одне ціле невід'ємне число n (0 ≤ n ≤ 2*10⁹).

Вихід. Кількість цифр у числі n.

Приклад входу	Приклад виходу
13243	5

РОЗВ’ЯЗОК

елементарна задача

Аналіз алгоритму

Кількість цифр у числі можна знайти:

· за допомогою одного циклу.

· за допомогою рекурсії, скориставшись рекурентним співвідношенням:

digits(n) =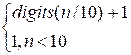

Реалізація алгоритму

Читаємо вхідне значення n. Якщо n = 0, то відповіддю буде 1. Інакше ініціалізуємо res нулем та підрахуємо кількість цифр у числі n.

scanf("%d",&n);

res = (n == 0);

while(n > 0)

{

n /= 10;

res++;

}

printf("%d\n",res);

Реалізація алгоритму – рекурсія

#include <stdio.h>

int n, res;

int digits(int n)

{

if (n < 10) return 1;

return 1 + digits(n / 10);

}

int main(void)

{

scanf("%d",&n);

res = digits(n);

printf("%d\n",res);

return 0;

}

Java реалізація

import java.util.*;

public class Main

{

static int digits(int n)

{

if (n < 10) return 1;

return 1 + digits(n / 10);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int res = digits(n);

System.out.println(res);

con.close();

}

}

Python реалізація

Перетворимо вхідне число n в рядок, після чого візьмемо його довжину.

n = int(input())

print(len(str(n)))

Якщо перед числом знаходяться проміжки, то наступна реалізація не є вірною:

s = str(input())

print(len(s))

Реалізація за допомогою циклу while:

x = int(input())

cnt = 0

if x == 0:

print ("1")

else:

while x > 0:

cnt += 1

x = x // 10

print (cnt)

Python реалізація – рекурсія

def f(n):

if n < 10:

return 1

return f(n / 10) + 1

n = int(input())

print (f(n))