42. Зеленое пятно
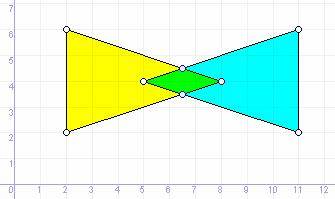
Два прожектора треугольной
формы образуют на стене два пятна, одно – голубого, а второе – желтого цвета.
Определить площадь пятна зеленого цвета, которое получится при наложении двух
пятен и форму (количество вершин) зеленого пятна.
Вход. В первой строке содержатся координаты одного пятна: x11, y11, x12,
y12, x13, y13,
а во второй – такие же координаты вершин второго пятна x21, y21,
x22, y22, x23,
y23. Известно, что -100
≤ xi, yi ≤ 100.
Выход. Вывести в одной
строке 2 числа: количество вершин зеленого пятна и, через пробел, его площадь
(с двумя знаками после запятой).
Пример входа
2 2 2 6 8 4
5 4 11 6 11
2
Пример
выхода
4 1.50
РЕШЕНИЕ
геометрия
Анализ алгоритма
Поскольку желтый и голубой
треугольники – выпуклые фигуры, то зеленое пятно будет иметь вид выпуклого
многоугольника. Его вершинами будут:
·
точки пересечения сторон треугольников
·
вершины треугольников, лежащие внутри других треугольников
Остается вычислить площадь
и количество вершин зеленого пятна.
Реализация алгоритма
При помощи правила Крамера
находим точку пересечения двух прямых.
int kramer(double a1,double b1, double c1,
double a2,double
b2, double c2,
double
*x, double *y)
{
double d = a1
* b2 - a2 * b1;
double dx = c1
* b2 - c2 * b1;
double dy = a1
* c2 - a2 * c1;
if (!d) return (dx == 0.0) + 1;
*x = dx/d; *y = dy/d;
return 0;
}
Ищем точку пересечения
отрезков [p1, p2] и [p3, p4],
записав их уравнения в параметрическом виде. Вычисляем параметры (t1, t2) точки пересечения. Отрезки пересекаются, если одновременно
0 ≤ t1 ≤ 1 и 0
≤ t2 ≤ 1.
int solve(pair<double,double> p1, pair<double,double> p2,
pair<double,double> p3, pair<double,double> p4,
double *xc, double
*yc)
{
double a1 =
p2.first - p1.first;
double b1 =
p3.first - p4.first;
double c1 =
p3.first - p1.first;
double a2 =
p2.second - p1.second;
double b2 =
p3.second - p4.second;
double c2 =
p3.second - p1.second;
double t1, t2;
int status =
kramer(a1,b1,c1,a2,b2,c2,&t1,&t2);
Если отрезки [p1, p2] и [p3, p4] не пересекаются, то
возвращаем 1. Значение status равно
0, если отрезки пересекаются.
if
(status || !((t1 >= 0.0) && (t1 <= 1.0)) ||
!((t2 >= 0.0) && (t2 <= 1.0))) return 1;
По
параметру t1 вычисляем координаты
точки пересечения отрезков в (xc, yc).
*xc = p1.first + (p2.first - p1.first) * t1;
*yc = p1.second + (p2.second - p1.second) *
t1;
return 0;
}
Вектор v будет хранить
координаты вершин зеленого пятна.
vector<pair<double,double> > v;
Добавляем вершину (x, y)
в зеленое пятно. Следует проверить, не находится ли она уже там (чтобы не
добавить одну и ту же вершину дважды).
void add(double x, double y)
{
int i;
for(i = 0; i
< v.size(); i++)
if ((fabs(v[i].first - x) < EPS)
&& (fabs(v[i].second - y) < EPS)) return;
v.push_back(make_pair(x,y));
}
Функция InTriangle возвращает истину, если
точка Point лежит внутри треугольника, вершины которого задаются
вектором m.
int InTriangle(pair<double,double> *m, pair<double,double> Point)
{
int i, res;
double ax, ay,
bx, by;
for(res = i =
0; i < 3; i++)
{
ax = m[i+1].first - m[i].first;
ay = m[i+1].second - m[i].second;
bx = Point.first - m[i+1].first;
by = Point.second - m[i+1].second;
res += sgn(ax * by - ay * bx);
}
return
(fabs(abs(res) - 3.0) < 1e-7);
}
Функция len2 возвращает
расстояние от точки p до начала
координат.
double len2(pair<double,double> p)
{
return p.first
* p.first + p.second * p.second;
}
Вычисление полярного угла точки p.
double PolarAngle(pair<double,double> p)
{
double res =
atan2(p.second,p.first);
return res;
}
Функция сортировки по полярному углу. Если углы точек a и b одинаковы, то
сортировка производится по расстоянию точек от начала координат (0, 0).
int f(pair<double,double> a, pair<double,double> b)
{
if
(fabs(PolarAngle(a) - PolarAngle(b)) < EPS) return
len2(a) < len2(b);
return PolarAngle(a) < PolarAngle(b);
}
Основная часть программы.
Считываем входные данные.
scanf("%lf %lf %lf %lf %lf %lf",&p1[0].first,&p1[0].second,&p1[1].first,
&p1[1].second, &p1[2].first,&p1[2].second);
p1[3] = p1[0];
scanf("%lf %lf %lf %lf %lf %lf",&p2[0].first,&p2[0].second,
&p2[1].first,&p2[1].second,&p2[2].first,&p2[2].second);
p2[3] = p2[0];
Находим координаты вершин зеленого пятна. Ищем точки пересечения сторон
двух заданных треугольников.
for(i = 0; i
< 3; i++)
for(j = 0; j
< 3; j++)
{
status = solve(p1[i],p1[i+1],p2[j],p2[j+1],&xc,&yc);
if (!status) add(xc,yc);
}
Перебираем вершины треугольников. Выясняем, какие из них лежат внутри
другого треугольника. Они будут принадлежать многоугольнику, который формирует
зеленое пятно.
for(i = 0; i
< 3; i++)
if(InTriangle(p1,p2[i]))
add(p2[i].first,p2[i].second);
for(i = 0; i
< 3; i++)
if(InTriangle(p2,p1[i]))
add(p1[i].first,p1[i].second);
Находим точку с наименьшей абсциссой и заносим ее в v[0].
for(i = 1; i
< v.size(); i++)
{
if (v[i].first < v[0].first)
swap(v[i],v[0]);
if ((v[i].first == v[0].first)
&& (v[i].second < v[0].second))
swap(v[i],v[0]);
}
Если ни одна точка не принадлежит зеленому пятну, то голубое и желтое
пятно не пересекаются. Площадь зеленого пятна равна нулю.
if (v.size()
== 0)
{
num = 0; s = 0;
printf("%d %.2lf\n",num,s);
return 0;
}
Голубое и желтое пятно пересекаются по отрезку. Площадь зеленого пятна
равна нулю.
if (v.size()
== 2)
{
num = 2; s = 0;
printf("%d %.2lf\n",num,s);
return 0;
}
Совершим параллельный перенос вершин зеленого пятна так, чтобы v[0] попало
в центр координат.
Center = v[0];
for(i = 0; i
< v.size(); i++)
v[i].first = v[i].first - Center.first,
v[i].second = v[i].second - Center.second;
Сортируем вершины зеленого пятна по полярному углу.
sort(v.begin()+1,v.end(),f);
Все точки из вектора v будут принадлежать выпуклой оболочке зеленого пятна.
Поэтому отдельно запускать алгоритм построения выпуклой оболочки нет
необходимости. Восстанавливаем координаты вершин многоугольника.
for(i = 0; i
< v.size(); i++)
v[i].first = v[i].first + Center.first,
v[i].second = v[i].second + Center.second;
По формуле трапеций вычисляем площадь многоугольника – зеленого пятна.
Если она равна 0, то голубой и желтый треугольники пересекаются в одной точке.
s = findArea(v); num = v.size();
if (fabs(s)
< 0.005) num = 1;
Выводим количество вершин num
зеленого пятна и его площадь s.
printf("%d
%.2lf\n",num,s);