48. Красные и синие квадраты

Петя и Вася готовились к контрольной работе по теме ”Периметр и площадь фигур”. Петя нарисовал геометрическую фигуру, закрасив на листе в клеточку некоторые клеточки синим цветом, а Вася вычислял периметр образованной фигуры и дорисовывал максимальное количество квадрато в красным цветом таким образом, чтобы периметр новообразованной фигуры оставался таким же.

Напишите программу, которая по заданным координатам закрашенных синих квадратов найдет максимальное количество красных квадратов, которое можно дорисовать так, чтобы периметр новообразованной фигуры не изменился.

Вход. В первой строке находится количество синих квадратов n (0 < n < 40404). Далее идут n строк, каждая из которых содержит координаты x, y (-101 ≤ x, y ≤ 101) левых нижних углов синих квадратов.

Каждый синий квадрат имеет хотя бы одну общую точку хотя бы с одним другим синим квадратом. Фигура, образованная синими квадратами, является связной.

Выход. Вывести количество красных квадратов.

Пример входа	Пример выхода
3 1 1 2 1 2 2	1

РЕШЕНИЕ

математика

Анализ алгоритма

Информацию о синих квадратах будем хранить в массиве m[220][220]. Поскольку нумерация ячеек в массиве в языке Си начинается с нуля, а в условии задачи присутствуют квадраты с отрицательными координатами, то совершим параллельный перенос координат квадратов так, чтобы центр (0, 0) перешел например в (110, 110).

Найдем периметр образовавшейся синей замкнутой (по условию) фигуры p. Найдем координаты левого нижнего (minx, miny) и правого верхнего (maxx, maxy) прямоугольника, ограничивающего синюю область.

Очевидно, что все пустые квадраты в ограничивающем прямоугольнике можно дорисовать красным – от этого периметр образованной фигуры не увеличится (он может или не измениться, или уменьшиться, если в синей области имеются дырки).

Если периметр ограничивающего прямоугольника pp меньше периметра синей области p, то следует дорисовать максимальное количество красных квадратов так, чтобы указанные периметры сравнялись. Очевидно, что значения периметров всегда четные. Если к прямоугольнику дорисовать колонку или ряд красных квадратов, то периметр полученного прямоугольника увеличится на 2. Поскольку условие задачи требует дорисовать максимальное количество красных квадратов, то каждый раз к имеющемуся прямоугольнику (изначально им является ограничивающий прямоугольник) следует пририсовывать ряд красных квадратов к той стороне, которая длиннее.

Пример

Рассмотрим следующий пример (фигура, образованная синими квадратами, является связной).

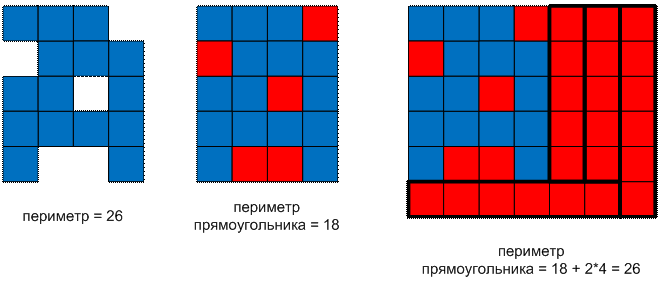
Периметр ограничивающего прямоугольника размером 5 * 4 равен 18, что меньше периметра синей области, равной 26. Добавляем сначала две колонки красных квадратов справа, после чего размер прямоугольника стал равен 5 * 6. Теперь длина прямоугольника стала больше ширины. Добавляем строку красных квадратов снизу. После чего все равно что добавить – или дополнительную строку, или дополнительный столбец. Периметр полученного прямоугольника сравнялся с периметром начальной синей области.

Реализация алгоритма

Объявим двумерный массив m, который будет содержать информацию о синих квадратах: m[i][j] = 1, если имеется синий квадрат с координатами (i, j).

#define MAX 220

int m[MAX][MAX];

Считываем входные данные. Совершаем параллельный перенос синих квадратов на вектор (110, 110). Вычисляем координаты прямоугольника (minx, miny) – (maxx, maxy), ограничивающего множество синих квадратов.

scanf("%d",&n); memset(m,0,sizeof(m));

minx = miny = 220; p = maxx = maxy = 0;

for(i = 0; i < n ; i++)

{

scanf("%d %d",&a,&b); a += 110; b += 110;

m[a][b] = 1;

if (a < minx) minx = a; if (a > maxx) maxx = a;

if (b < miny) miny = b; if (b > maxy) maxy = b;

}

Вычисляем периметр p синей фигуры. Для этого необходимо просмотреть все синие квадраты и прибавлять единицу каждый раз, когда слева (справа, сверху, снизу) от него имеется пустая клетка.

for(i = 1; i < MAX - 1; i++)

for(j = 1; j < MAX - 1; j++)

if (m[i][j])

{

if (m[i-1][j] == 0) p++;

if (m[i+1][j] == 0) p++;

if (m[i][j+1] == 0) p++;

if (m[i][j-1] == 0) p++;

}

Вычислим размеры ограничивающего прямоугольника a и b. В переменную pp занесем его периметр, а в res количество красных квадратов, которое можно нарисовать в ограничивающем прямоугольнике.

a = maxx - minx + 1; b = maxy - miny + 1;

pp = 2 * (a + b); res = a * b - n;

Если периметр ограничивающего прямоугольника pp меньше периметра синей области p, то следует продолжать процесс закрашивания квадратов.

while(pp < p)

{

Переменные a и b содержат длины сторон прямоугольника. Положим a < b.

if (a > b) temp = a, a = b, b = temp;

Дорисуем к стороне длины b ряд красных квадратов. Получим прямоугольник со сторонами a + 1 и b, периметр которого на два больше предыдущего.

res += b; pp += 2; a++;

}

Выводим результат.

printf("%d\n",res);