50. Разрезанное число

Василий на бумажке в виде полоски написал число, кратное d. Его младший брат Дмитрий разрезал число на k частей. Василий решил восстановить написанное число, но столкнулся с проблемой. Он помнил только число d, а чисел, кратных d, можно сложить несколько.

Сколько чисел, кратных числу d, может составить Василий, если составляя исходное число, он использует все части.

Вход. В первой строке записано два числа d и k (1 ≤ k < 9, 1 ≤ d ≤ 100). В следующих k строках находятся части числа. Количество цифр в разрезанных частях не превышает 10.

Выход. Выведите количество разных чисел, кратных d.

Пример входа	Пример выхода
5 3 13 85 45	4

РЕШЕНИЕ

комбинаторика - перестановки

Анализ алгоритма

Занесем числа всех частей в массив. Рассмотрим все возможные склейки имеющиеся частей. Такой перебор возможен, так как k < 9 и разных склеек будет не более 9!. Для каждого полученного склейкой числа проверяем, делится ли оно на d.

Пример

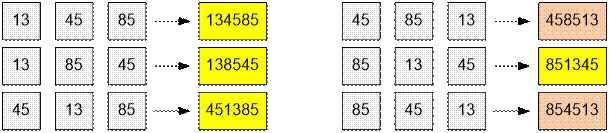
Рассмотрим все возможные склейки трех частей 13, 85 и 45. Для каждого полученного числа проверяем, делится ли оно на d = 5.

Реализация алгоритма

Функция f возвращает значение 10^k, где k – количество цифр в числе n.

long long f(long long n)

{

long long res = 1;

while (n > 0)

{

res *= 10;

n /= 10;

}

return res;

}

Основная часть программы. Числа, записанные в частях бумажки, занесем в массив v.

scanf("%d %d", &d, &k);

for (c = i = 0; i < k; i++)

{

scanf("%lld", &value);

v.push_back(value);

}

Отсортируем числа, записанные на частях.

sort(v.begin(), v.end());

Перебираем все возможные перестановки частей при помощи next_permutation. В переменной value вычисляем остаток от деления склеенного числа на d.

do

{

for (i = value = 0; i < k; i++)

К числу value справа приписываем v[i].

value = (value * f(v[i]) + v[i]) % d;

Если полученное склеенное число value делится на d, то увеличиваем счетчик c на 1.

if (value % d == 0) c++;

} while (next_permutation(v.begin(), v.end()));

Выводим ответ.

printf("%d\n", c);