68. Метро

Схема метро состоит из n станций, расположенных l на  линиях. Каждая станция принадлежит одной или нескольким линиям (в этом случае на станции можно выполнить пересадку на любую из проходящих через неё линий). Каждая линия включает не менее двух станций и пересекается хотя бы с одной другой линией. Схема метро является связной.

Передвижение между двумя соседними станциями одной линии возможно в обоих направлениях и занимает 2 минуты. Пересадка с одной линии на другую в пределах одной станции занимает 1 минуту. Другими затратами времени можно пренебречь.

Определите минимальное время, необходимое менеджеру фирмы «Диез-продукт», чтобы добраться от станции a до здания офиса компании, расположенного рядом со станцией b.

Вход. В первой строке заданы два натуральных числа n и l (1 ≤ l ≤ 10). В следующих l строках указаны последовательные номера станций каждой из линий метро. В последней строке заданы номера и линии начальной и конечной станций. Все числа натуральные и не превышают 70.

Выход. Выведите минимальное время движения между указанными станциями.

Пример входа	Пример выхода
7 3 2 1 3 6 1 4 5 5 7 2 1 7 3	10

РЕШЕНИЕ

графы – алгоритм Дейкстры

Анализ алгоритма

Кратчайшее расстояние от источника до вершины v, принадлежащей линии l, храним в dist[v][l], где 1 ≤ v ≤ 70, 1 ≤ l ≤ 10. Граф храним в виде списков смежности. Вместе с направлением и стоимостью ребра храним номер линии метро, которой принадежит вершина куда направлено ребро.

Стартуем со станции s, находящейся на линии line1. Ответ на задачу – минимальная стоимость, за которую можно добраться до вершины f на линии line2. При движении между вершинами следует совершить проверку: если вершины принадлежат разным линиям, то следует добавить 1 (совершить пересадку).

При помощи алгоритма Дейкстры находим кратчайшее расстояния из сосотяния (s, line1) в (f, line2).

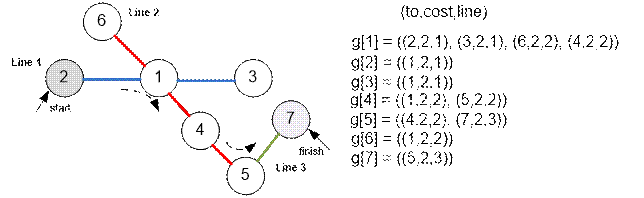
Пример

В приведенном примере необходимо найти кратчайший маршрут от станции 2 на линии 1 до станции 7 на линии 3.

· Идём по линии 1 от станции 2 к станции 1: 2 минуты.

· Совершаем пересадку на станции 1 с линии 1 на линию 2: 1 минута.

· Идём по линии 2 от станции 1 к станции 5: 4 минуты.

· Совершаем пересадку на станции 5 с линии 2 на линию 3: 1 минута.

· Идём по линии 3 от станции 5 к станции 7: 2 минуты.

Итого весь путь займет 10 минут.

Реализация алгоритма

Количество вершин в графе не более MAX = 71. Количество линий не более LINES = 11.

#define MAX 71

#define LINES 11

Кратчайшее расстояние от источника до вершины v, принадлежащей линии l, храним в dist[v][l]. Объявим массив кратчайших расстояний.

int dist[MAX][LINES];

Структура node содержит информацию о ребре:

· to – направление ребра;

· cost – стоимость ребра;

· line – какой линии метро ребро принадлежит;

struct node

{

int to, cost, line;

node(int to, int cost, int line) : to(to), cost(cost), line(line) {}

};

Структура node также будет использоваться в очереди с приоритетами, где

· to – текущая вершина;

· cost – минимальная стоимость проезда до вершины to (на линии line);

· line – номер линии метро, на которой находится вершина to;

В очереди с приоритетами вершины сортируются по возрастанию стоимости проезда.

bool operator< (node a, node b)

{

return a.cost > b.cost;

}

Список смежности вершин графа.

vector<vector<node> > g;

Основная часть программы. Читаем входные данные.

scanf("%d %d", &n, &l);

g.resize(n + 1);

Читаем i-ую линию метро. Время движения между соседними станциями u и v равно 2.

for (i = 1; i <= l; i++)

{

Читаем станцию u – первую станцию i-ой линии метро. За станцией u идет станция v.

scanf("%d ", &u);

while (scanf("%d%c", &v, &ch))

{

Движение возможно в обоих направлениях. Стоимость ребра равна 2.

g[u].push_back(node(v, 2, i));

g[v].push_back(node(u, 2, i));

u = v;

Как только доходим до конца строки – заканчиваем читать данные очередной линии метро.

if (ch == '\n') break;

}

}

Инициализируем массив кратчайших расстояний.

for (i = 1; i <= n; i++)

for (j = 1; j <= l; j++)

dist[i][j] = 2000000000;

Читаем информацию о начальной и конечной станции. Для каждой станции задается линия, которой она принадлежит.

scanf("%d %d %d %d", &s, &line1, &f, &line2);

Стартуем со станции s, находящейся на линии line1.

dist[s][line1] = 0;

priority_queue<node, vector<node> > pq;

Заносим в очередь структуру node, содержащую начальную вершину s на линии line1. Стоимость попадания в начальную вершину равна 0.

pq.push(node(s, 0, line1)); // (v, cost, line)

while (!pq.empty())

{

Извлекаем из очереди вершину v с наименьшей стоимостью.

int cost = pq.top().cost;

int v = pq.top().to;

int l1 = pq.top().line;

pq.pop(); // dist[v][l1] = cost

Перебираем вершины, связанные с v.

for (i = 0; i < g[v].size(); i++)

{

Имеется ребро v – to стоимостью w, принадлежащее линии l2.

int to = g[v][i].to;

int w = g[v][i].cost;

int l2 = g[v][i].line;

Если двигаться в to по ребру v – to, то стоимость составит cost + w.

int tot_cost = cost + w;

Если линии у вершин v и to разные, то следует совершить пересадку с линии l1 на линию l2.

if (l1 != l2) tot_cost += 1;

Если движение по ребру v – to дает лучший результат, то улучшаем значение dist[to][l2] и заносим вершину to в очередь (стоимость попадания в нее составляет tot_cost и она находится на линии l2).

if (tot_cost < dist[to][l2])

{

dist[to][l2] = tot_cost;

pq.push(node(to, tot_cost, l2));

}

}

}

Вывод ответа – стоимости добраться до вершины f на линии line2.

printf("%d\n", dist[f][line2]);