68. Metro

The metro system consists of n stations located on l lines. Each station belongs to one or several lines (in this case, a passenger can transfer to any of the lines passing through this station). Each line includes at least two stations and intersects with at least one other line. The metro network is connected.

Travel between two adjacent stations on the same line is possible in both directions and takes 2 minutes. A transfer from one line to another within the same station takes 1 minute. Other time costs can be neglected.

Determine the minimum time required for the manager of the company “Diez-Product” to travel from station a to the company’s office located near station b.

Input. The first line contains two positive integers n and l (1 ≤ l ≤ 10). Each of the next l lines lists the consecutive station numbers of each metro line. The last line contains the numbers and line indices of the starting and destination stations. All numbers are positive and do not exceed  70.

Output. Print the minimum travel time between the specified stations.

Sample input	Sample output
7 3 2 1 3 6 1 4 5 5 7 2 1 7 3	10

SOLUTION

graphs – Dijkstra

Algorithm analysis

The shortest distance from the source to a vertex v belonging to line l is stored in dist[v][l], where 1 ≤ v ≤ 70 and 1 ≤ l ≤ 10. The graph is represented as an adjacency list. For each edge, in addition to its direction and cost, the number of the metro line to which the destination vertex belongs is also stored.

The algorithm starts from station s, located on line line1. The goal is to find the minimum travel cost required to reach station f, which lies on line line2.

When moving between vertices, it is necessary to check whether they belong to the same line: if the lines differ, an additional cost of 1 is added (representing a line transfer).

Using Dijkstra’s algorithm, we find the shortest distance from state (s, line1) to state (f, line2).

Example

In the given example, it is required to find the shortest route from station 2 on line 1 to station 7 on line 3.

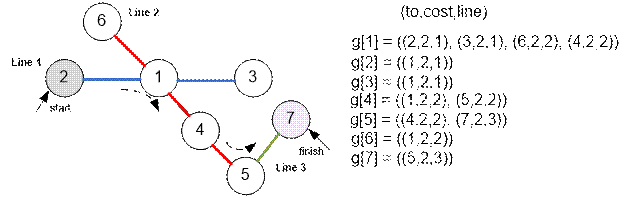
· Move along line 1 from station 2 to station 1: 2 minutes.

· Transfer at station 1 from line 1 to line 2: 1 minute.

· Move along line 2 from station 1 to station 5: 4 minutes.

· Transfer at station 5 from line 2 to line 3: 1 minute.

· Move along line 3 from station 5 to station 7: 2 minutes.

Thus, the entire trip takes 10 minutes.

Algorithm implementation

The number of vertices in the graph does not exceed MAX = 71. The number of metro lines does not exceed LINES = 11.

#define MAX 71

#define LINES 11

The shortest distance from the source to a vertex v belonging to line l is stored in dist[v][l]. We declare an array to store the shortest distances.

int dist[MAX][LINES];

The structure node contains information about an edge:

· to is the destination vertex;

· cost is the cost of the edge;

· line is the metro line to which the edge belongs;

struct node

{

int to, cost, line;

node(int to, int cost, int line) : to(to), cost(cost), line(line) {}

};

The node structure is also used in the priority queue, where:

· to is the current vertex;

· cost is the minimum travel cost to reach vertex to (on line line);

· line is the metro line number on which vertex to is located.

In the priority queue, vertices are ordered by increasing travel cost.

bool operator< (node a, node b)

{

return a.cost > b.cost;

}

Declare an adjacency list to represent the graph.

vector<vector<node> > g;

The main part of the program. Read the input data.

scanf("%d %d", &n, &l);

g.resize(n + 1);

Read the i-th metro line. The travel time between two consecutive stations u and v is 2.

for (i = 1; i <= l; i++)

{

Read station u – the first station of the i-th metro line. The next station after u is v.

scanf("%d ", &u);

while (scanf("%d%c", &v, &ch))

{

Movement between stations is possible in both directions, and the cost of each edge is 2.

g[u].push_back(node(v, 2, i));

g[v].push_back(node(u, 2, i));

u = v;

Once the end of the line description is reached, we stop reading data for the current metro line.

if (ch == '\n') break;

}

}

Initialize the array for storing the shortest distances.

for (i = 1; i <= n; i++)

for (j = 1; j <= l; j++)

dist[i][j] = 2000000000;

Read the information about the starting and destination stations. For each station, the metro line it belongs to is specified.

scanf("%d %d %d %d", &s, &line1, &f, &line2);

The algorithm starts from station s, located on line line1.

dist[s][line1] = 0;

Insert into the priority queue a node structure containing the starting vertex s on line line1. The cost of reaching the starting vertex is 0.

priority_queue<node, vector<node> > pq;

pq.push(node(s, 0, line1)); // (v, cost, line)

while (!pq.empty())

{

Extract from the priority queue the vertex v with the minimum cost.

int cost = pq.top().cost;

int v = pq.top().to;

int l1 = pq.top().line;

pq.pop(); // dist[v][l1] = cost

Iterate over all vertices adjacent to v.

for (i = 0; i < g[v].size(); i++)

{

Consider the edge v → to with cost w, which belongs to line l2.

int to = g[v][i].to;

int w = g[v][i].cost;

int l2 = g[v][i].line;

If we move along the edge v → to, the total cost of the path becomes cost + w.

int tot_cost = cost + w;

If vertices v and to belong to different lines, a transfer from line l1 to line l2 must be made.

if (l1 != l2) tot_cost += 1;

If moving along the edge v → to improves the current value, update dist[to][l2] and insert vertex to into the queue (its total cost is tot_cost, and it is located on line l2).

if (tot_cost < dist[to][l2])

{

dist[to][l2] = tot_cost;

pq.push(node(to, tot_cost, l2));

}

}

}

Print the result – the minimum travel cost to reach vertex f on line line2.

printf("%d\n", dist[f][line2]);