932. Высота треугольника

Определить высоту треугольника площадью S, если его основание больше высоты на величину a.

Вход. Два целых числа: S (0 < S ≤ 100), и a (|a| ≤ 100).

Выход. Искомая высота с точностью до сотых.

Пример входа	Пример выхода
15 1	5.00

РЕШЕНИЕ

геометрия - базовая

Анализ алгоритма

Пусть h – высота треугольника. Тогда его основание равно h + a. Площадь треугольника равна S = ½ h (h + a). Значения S и a заданы, решаем квадратное уравнение относительно h:

h² + ha – 2S = 0,

дискриминант D = a² + 4S,

положительный корень равен h =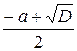

Реализация алгоритма

Читаем входные данные. Решаем квадратное уравнение S = ½ h (h + a) относительно h и выводим его положительный корень.

scanf("%lf %lf",&s,&a);

d = a*a + 8*s;

h = (-a + sqrt(d)) / 2;

printf("%.2lf\n",h);

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

double s = con.nextDouble();

double a = con.nextDouble();

double d = a * a + 8 * s;

double h = (-a + Math.sqrt(d)) / 2;

System.out.println(h);

con.close();

}

}

Python реализация

import math

s, a = map(float,input().split())

d = a*a + 8*s;

h = (-a + math.sqrt(d)) / 2;

print("%.2f" %h)